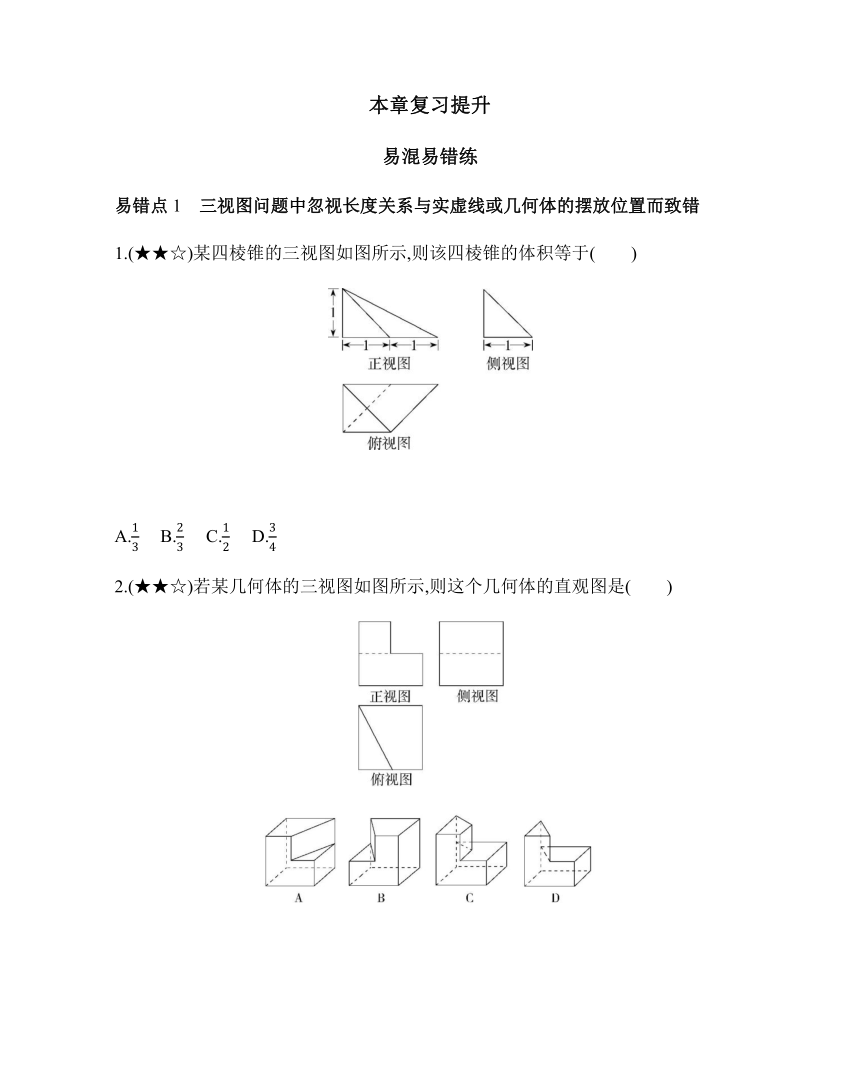
本章复习提升 易混易错练 易错点1 三视图问题中忽视长度关系与实虚线或几何体的摆放位置而致错 1.(★★)某四棱锥的三视图如图所示,则该四棱锥的体积等于( ) A. B. C. D. 2.(★★)若某几何体的三视图如图所示,则这个几何体的直观图是( ) 易错点2 求几何体的表面积时考虑不全致错 3.(★★)一个机器零件的三视图如图所示,其中侧视图是一个半圆与边长为a的正方形,俯视图是一个半圆内切于边长为a的正方形.若该机器零件的表面积为96+4π,则a的值为( ) A.4 B.2 C.8 D.6 4.(★★)如图,网格纸上正方形小格的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为 ( ) A.20π B.24π C.28π D.32π 易错点3 对几何体分类讨论不全致错 5.(★★)球的一个内接圆锥满足:球心到该圆锥底面的距离是球半径的一半,则该圆锥的体积和此球体积的比值为 . 6.(★★)已知半径为5的球O被两平行平面所截,两截面圆的半径分别为3和4,求分别以两截面为上、下底面的圆台的侧面积. 思想方法练 一、函数与方程思想在求表面积、体积中的应用 1.(★★★)如图,网格纸上正方形小格的边长为1,图中粗实(虚)线画出的是某三棱锥的三视图,则该三棱锥的外接球的表面积为( ) A.π B.6π C.11π D.12π 2.(★★)一个圆锥的底面半径为2 cm,高为6 cm,在其内部有一个高为x cm的内接圆柱. (1)求圆锥的侧面积; (2)当x为何值时,圆柱的侧面积最大 并求出侧面积的最大值. 3.(★★)如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,求三棱锥P-DCE的外接球的体积. 二、转化与化归思想在求体积或距离中的应用 4.(★★)如图,△ABC中,AB=8,BC=10,AC=6,DB垂直于平面ABC,且AE∥FC∥BD,BD=3,FC=4,AE=5,求此几何体的体积. 5.(★★)如图所示的三棱锥O-ABC为长方体的一角.其中OA、OB、OC两两垂直,三个侧面OAB、OAC、OBC的面积分别为1.5 cm2、1 cm2、3 cm2,求三棱锥O-ABC的体积. 6.(★★)在棱长为a的正方体ABCD-A1B1C1D1中,求A到平面A1BD的距离d. 答案全解全析 易混易错练 1.A 抠点法.在长方体ABCD-A1B1C1D1中抠点, (1)由正视图可知:C1D1上没有点; (2)由侧视图可知:B1C1上没有点; (3)由俯视图可知:CC1上没有点; (4)由正(俯)视图可知:D,E处有点,由俯视图中虚线可知B,F处有点,A点排除. 由上述可还原出四棱锥为A1-BEDF,如图所示. S四边形BEDF=1×1=1,=×1×1=.故选A. 2.D A的正视图和俯视图不符合要求,B的正视图和侧视图不符合要求,C的俯视图显然也不符合要求. 3.A 该几何体为一个正方体与四分之一个球的组合体,所以表面积为6a2+×4π×=96+4π,所以a=4. 4.C 由三视图可知该几何体是一个圆柱和一个圆锥的组合体,其表面积为π×3×5+2π×1×2+π×32=28π.故选C. 5.答案 或 解析 如图所示,设球的半径为r,则球心到该圆锥底面的距离为,于是圆锥的底面半径为=,高为或.若高为,则该圆锥的体积为×π××=πr3,球的体积为πr3,∴该圆锥的体积和此球体积的比值为=.同理可得高为时,比值为. 6.解析 ①当两截面圆在球心O的同侧时,如图(1)所示,AB为较大的截面圆的直径,O1为较大的截面圆的圆心,CD为较小的截面圆的直径,O2为较小的截面圆的圆心,梯形ABDC为圆台的轴截面,由题意,知OO1=3,OO2=4,则圆台的高为O1O2=1,AC=,所以圆台的侧面积S侧=π(3+4)×=7π. 图(1) ②当两截面圆在球心O的异侧时,如图(2)所示,AB为较大的截面圆的直径,O1为较大的截面圆的圆心,CD为较小的截面圆的直径,O2为较小的截面圆的圆心,梯形ABDC为圆台的轴截面,由题意,知OO1=3,OO2=4,则圆台的高为O1O2=7,AC=5,所以圆台的侧面积为S侧=π(3+4)×5=35π. 图(2) 思 ... ...
~~ 您好,已阅读到文档的结尾了 ~~