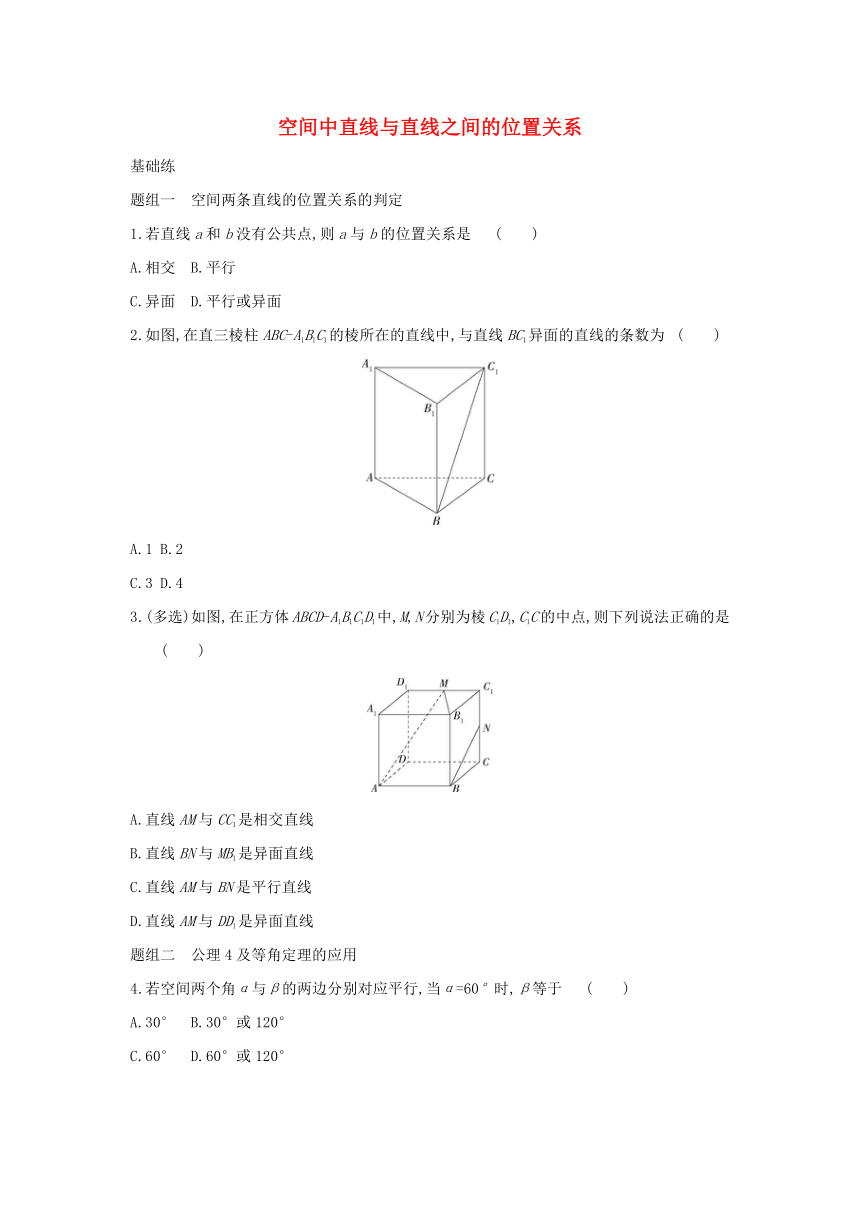
空间中直线与直线之间的位置关系 基础练 题组一 空间两条直线的位置关系的判定 1.若直线a和b没有公共点,则a与b的位置关系是 ( ) A.相交 B.平行 C.异面 D.平行或异面 2.如图,在直三棱柱ABC-A1B1C1的棱所在的直线中,与直线BC1异面的直线的条数为 ( ) A.1 B.2 C.3 D.4 3.(多选)如图,在正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,则下列说法正确的是 ( ) A.直线AM与CC1是相交直线 B.直线BN与MB1是异面直线 C.直线AM与BN是平行直线 D.直线AM与DD1是异面直线 题组二 公理4及等角定理的应用 4.若空间两个角α与β的两边分别对应平行,当α=60°时,β等于 ( ) A.30° B.30°或120° C.60° D.60°或120° 5.如图,在四面体A-BCD中,M,N,P,Q,E分别是AB,BC,CD,DA,AC的中点,则下列说法不正确的是 ( ) A.M,N,P,Q四点共面 B.∠QME=∠CBD C.△BCD∽△MEQ D.四边形MNPQ为梯形 6.如图,已知在棱长为a的正方体A1B1C1D1-ABCD中,M,N分别是棱CD,AD的中点.求证: (1)四边形MNA1C1是梯形; (2)∠DNM=∠D1A1C1. 题组三 异面直线所成的角 7.如图,在直三棱柱ABC-A1B1C1中,D为A1B1的中点,AB=BC=2,BB1=1,AC=2,则异面直线BD与AC所成的角为 ( ) A.30° B.45° C.60° D.90° 8.(2021湖南长沙雅礼教育集团高二上期中)如图,正方体ABCD-A1B1C1D1中,AC与BC1所成角的大小是 . 提升练 一、选择题 1.空间中有三条线段AB,BC,CD,且∠ABC=∠BCD,那么直线AB与CD的位置关系是 ( ) A.平行 B.异面 C.相交或平行 D.平行或异面或相交 2.设P是直线l外一定点,过点P且与l成60°角的异面直线 ( ) A.有无数条 B.有两条 C.至多有两条 D.仅有一条 3.一个正方体纸盒展开后如图所示,在原正方体纸盒中有下列结论:①AB⊥EF;②AB与CM成60°角;③EF与MN是异面直线;④MN∥CD,其中正确的是 ( ) A.①③ B.③④ C.②③ D.①② 二、填空题 4.如图,点P,Q,R,S分别在正方体的四条棱上,且是所在棱的中点,则直线PQ与RS是异面直线的图是 (填序号). 5.在正方体ABCD-A1B1C1D1中,M,N分别是棱CD,CC1的中点,则异面直线A1M与DN所成角的大小是 . 三、解答题 6.如图,在四棱柱ABCD-A1B1C1D1中,侧面都是矩形,底面ABCD是菱形,且AB=BC=2,∠ABC=120°,若异面直线A1B和AD1所成的角为90°,试求AA1的长度. 7.正三棱锥S-ABC的侧棱长与底面边长都为a,E,F分别是SC,AB的中点,求异面直线EF和SA所成的角. 参考答案: 基础练 1.D 2.C 3.BD 4.D 5.D 7.C 1.D 因为两直线相交只有一个公共点,两直线平行或异面没有公共点,所以选D. 2.C 在直三棱柱ABC-A1B1C1的棱所在的直线中,与直线BC1异面的直线有A1B1,AC,AA1,共3条.故选C. 3.BD ∵A,M,C,C1四点不共面, ∴直线AM与CC1是异面直线,故A中说法错误; 直线BN与MB1不同在任何一个平面内,是异面直线,故B中说法正确; 直线AM与BN不同在任何一个平面内,是异面直线,故C中说法错误; 直线AM与DD1不同在任何一个平面内,是异面直线,故D中说法正确.故选BD. 4.D ∵空间两个角α与β的两边分别对应平行,∴这两个角相等或互补, ∵α=60°,∴β=60°或β=120°.故选D. 5.D 由中位线定理,易知MQ∥BD,ME∥BC,QE∥CD,NP∥BD.对于A,由公理4易得MQ∥NP,所以M,N,P,Q四点共面,故A中说法正确;根据等角定理,得∠QME=∠CBD,∠MEQ=∠BCD,所以△BCD∽△MEQ,故B、C中说法正确;由三角形的中位线定理及公理4,知MQNP,所以四边形MNPQ为平行四边形,故D中说法不正确.故选D. 6.证明 (1)如图,连接AC,在△ACD中, M,N分别是CD,AD的中点, ∴MN是△ACD的中位线, ∴MN∥AC,且MN=AC. 由正方体的性质得AC∥A1C1,AC=A1C1, ∴MN∥A1C1,MN=A1C1,即MN≠A1C1, ∴四边形MNA1C1是梯形. (2)由(1)可知MN∥A1C1.又ND∥A1D1, ... ...
~~ 您好,已阅读到文档的结尾了 ~~

