高教版《电工基础》 第九章 相量法教案

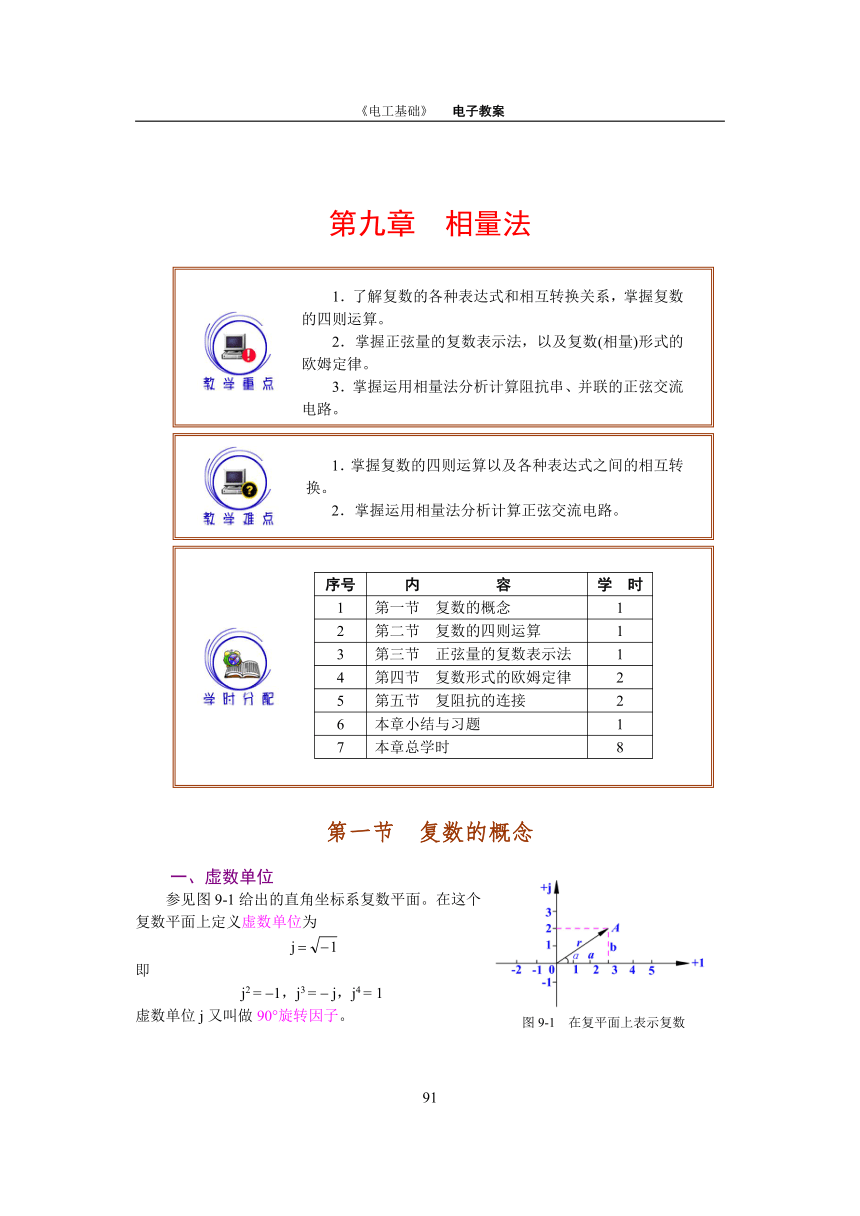
《电工基础》 电子教案 相量法 序号 内　　　　　容 学　时 1 第一节　复数的概念 1 2 第二节　复数的四则运算 1 3 第三节　正弦量的复数表示法 1 4 第四节　复数形式的欧姆定律 2 5 第五节　复阻抗的连接 2 6 本章小结与习题 1 7 本章总学时 8 第一节 复数的概念 一、虚数单位 参见图9-1给出的直角坐标系复数平面。在这个 复数平面上定义虚数单位为 即 j2 = 1，j3 = j，j4 = 1 虚数单位j又叫做90旋转因子。 二、复数的表达式 　　一个复数Z有以下四种表达式。 1．直角坐标式(代数式) Z = a + jb 式中，a叫做复数Z的实部，b叫做复数Z的虚部。 在直角坐标系中，以横坐标为实数轴，纵坐标为虚数轴，这样构成的平面叫做复平面。任意一个复数都可以在复平面上表示出来。例如复数A = 3 + j2在复平面上的表示如图9-1所示。 2．三角函数式 在图9-1中，复数Z与x轴的夹角为 ，因此可以写成 Z = a + jb = |Z|(cos jsin) 式中|Z|叫做复数Z的模，又称为Z的绝对值，也可用r表示，即 叫作复数Z的辐角，从图9-1中可以看出 复数Z的实部a、虚部b与模|Z|构成一个直角三角形。 3．指数式 利用欧拉公式，可以把三角函数式的复数改写成指数式，即 Z =|Z|(cos jsin) =|Z|ej 4．极坐标式(相量式) 复数的指数式还可以改写成极坐标式，即 Z =|Z|/ 以上这四种表达式是可以相互转换的，即可以从任一个式子导出其它三种式子。 解：利用关系式Z = a + jb =|Z|/ ，|Z|=， = arctan，计算如下： (1) Z1= 2 = 2/0 (2) Z2 = j5 = 5/90 (j代表90旋转因子，即将“5”作反时针旋转90) 　 (3) Z3 = j9 = 9/90 (－j代表－90旋转因子，即将“9”作顺时针旋转90) 　　(4) Z4= 10 = 10/180或10/180 (“”号代表 180) (5) Z5 = 3 + j4 = 5/53.1 (6) Z6 = 8 j6 = 10/36.9 (7) Z7 = 6 + j8 = (6 j8) = (10/ 53.1) = 10/180 53.1 = 10/126.9 (8) Z8 = 8 j6 = (8 + j6) = (10/36.9) = 10/180 + 36.9 = 10/143.1。 解：利用关系式Z = |Z|/ =|Z|(cos + jsin) = a + jb计算： Z1= 20/53.1 = 20(cos53.1 + jsin53.1) = 20(0.6 + j0.8) = 12 + j16 Z2 = 10/36.9 = 10(cos36.9 jsin36.9) = 10(0.8 j0.6) = 8 j6 Z3 = 50/120 = 50(cos120 + jsin120) = 50( 0.5 + j0.866) = 25 + j43.3 Z4 = 8/ 120 = 8(cos120 jsin120) = 8( 0.5 j0.866) = 4 j6.928　 第二节 复数的四则运算 设Z1= a + jb =|Z1|/ ，Z2 = c + jd = |Z2|/ ，复数的运算规则为 1．加减法 Z1 Z2 = (a c) + j(b d) 2．乘法 Z1 · Z2 = |Z1| · |Z2|/ + 3．除法 / 4．乘方 /n 　　 解：(1) Z1 + Z2 = (8 j6) + (3 + j4) = 11 j2 = 11.18/10.3 　　(2) Z1 Z2 = (8 j6) (3 j4) = 5 j10 = 11.18/ 63.4 　　(3) Z1 · Z2 = (10/ 36.9) (5/53.1) = 50/16.2 (4) Z1 / Z2 = (10/ 36.9) (5/53.1) = 2/ 90　 第三节　正弦量的复数表示法 正弦量可以用复数表示，即可用振幅相量或有效值相量表示，但通常用有效值相量表示。其表示方法是用正弦量的有效值作为复数相量的模、用初相角作为复数相量的辐角。 正弦电流i = Imsin( t i)的相量表达式为 I/i 正弦电压u = Umsin( t u)的相量表达式为 = U/u 解：(1) 正弦电压u的有效值为U = 0.7071 311 = 220 V，初相 u = 30，所以它的相量为 U/u = 220/30 V 　 (2) 正弦电流i的有效值为I = 0.7071 4.24 = 3 A，初相i = 45，所以它的相量为 I=I/i = 3/45 A 解: u =sin( t 37) V，i = 5sin( t + 60) A　。 解: 首先用复数相量表示正弦量i1、i2，即 3/30 A = 3(cos30 + jsin30) = 2.598 j1.5 A 4/60 A = 4(cos60 jsin60) = 2 j3.464 A 然后作复数加法：4.598 j1.964 = 5/23.1 A 　　最后将结果还原成正弦量：i1 i2 =sin( t 23.1) A 第四节　复数形式的欧姆定律 一、复数形式的欧姆定律 定义复阻抗 ... ...