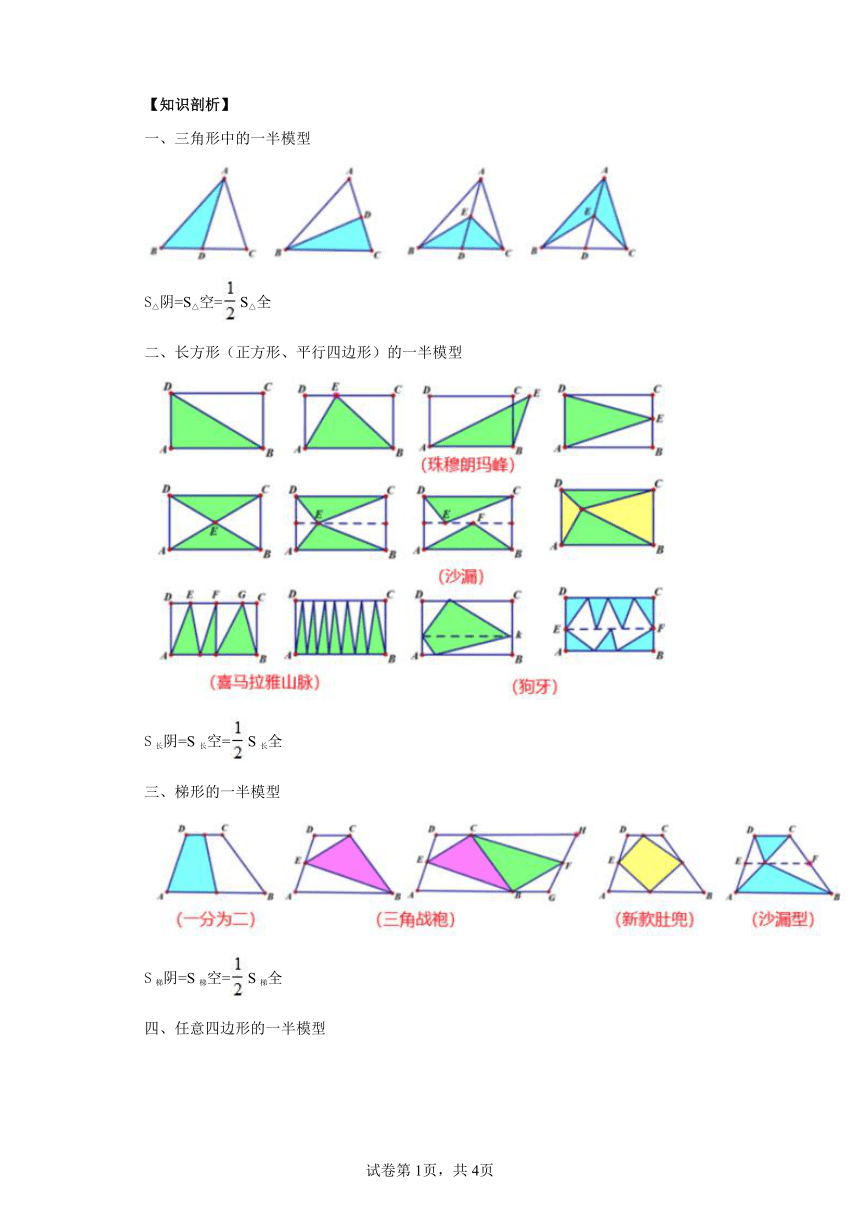
【知识剖析】 一、三角形中的一半模型 S△阴=S△空=S△全 二、长方形(正方形、平行四边形)的一半模型 S长阴=S长空=S长全 三、梯形的一半模型 S梯阴=S梯空=S梯全 四、任意四边形的一半模型 S四阴=S四空=S四全 【基础巩固】 1.如图所示,正方形的边长为厘米,长方形的长为厘米,那么长方形的宽为几厘米? 2.如图,三角形ABC的面积是24,D、E和F分别是BC、AC和AD的中点.求三角形DEF的面积. 3.如图所示,在长方形内有四条线段把长方形分成若干块,已知有三块图形的面积分别是13、35、49,那么图中阴影部分的面积是多少 4.下图中长方形的长是20,宽是12,求它的内部阴影部分面积. 5.在边长为6厘米的正方形内任取一点,将正方形的一组对边二等分,另一组对边三等分,分别与点连接,求阴影部分面积. 6.一个长方形分成4个不同的三角形,绿色三角形面积占长方形面积的,黄色三角形面积是.问:长方形的面积是多少平方厘米? 7.是长方形内一点,已知的面积是,的面积是,求的面积是多少? 8.如图,已知长方形的面积,三角形的面积是,三角形的面积是,那么三角形的面积是多少? 【勇攀高峰】 9.如图,正方形的边长为10,四边形的面积为5,那么阴影部分的面积是多少? 10.如右图所示,在梯形中,、分别是其两腰、的中点,是上的任意一点,已知 的面积为,而的面积恰好是梯形面积的,则梯形的面积是( ). 试卷第1页,共3页 试卷第1页,共3页 参考答案: 1.6.4 【详解】 本题主要是让学生会运用等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形).三角形面积等于与它等底等高的平行四边形面积的一半. 证明:连接.(我们通过把这两个长方形和正方形联系在一起). ∵在正方形中,边上的高, ∴(三角形面积等于与它等底等高的平行四边形面积的一半) 同理,. ∴正方形与长方形面积相等. 长方形的宽(厘米). 2.3 【详解】三角形ADC的面积是三角形ABC面积的一半, 三角形ADE又是三角形ADC面积的一半. 三角形FED的面积是三角形ADE面积的一半,所以三角形FED的面积. 3.解:设长方形的面积为S,则 由图形可知, 【详解】略 4.120 【详解】ABEF也是一个长方形,它内部的三个三角形阴影部分高都与BE一样长. 而三个三角形底边的长加起来,就是FE的长.因此这三个三角形的面积之和FE×BE÷2, 它恰好是长方形ABEF面积的一半. 同样道理,FECD也是长方形,它内部三个三角形(阴影部分)面积之和是它的面积的一半. 因此所有阴影的面积是长方形ABCD面积的一半,也就是20×12÷2=120. 5.15 【详解】 (法1)特殊点法.由于是正方形内部任意一点,可采用特殊点法,假设点与点重合,则阴影部分变为如上中图所示,图中的两个阴影三角形的面积分别占正方形面积的和,所以阴影部分的面积为平方厘米. (法2)连接、. 由于与的面积之和等于正方形面积的一半,所以上、下两个阴影三角形的面积之和等于正方形面积的,同理可知左、右两个阴影三角形的面积之和等于正方形面积的,所以阴影部分的面积为平方厘米. 6.60 【详解】黄色三角形与绿色三角形的底相等都等于长方形的长,高相加为长方形的宽,所以黄色三角形与绿色三角形的面积和为长方形面积的,而绿色三角形面积占长方形面积的,所以黄色三角形面积占长方形面积的. 已知黄色三角形面积是,所以长方形面积等于(). 7.3 【详解】由于是长方形,所以,而,所以,则,所以. 8.6.5 【详解】 方法一:连接对角线. ∵是长方形 ∴ ∴, ∴, ∴ ∴. 方法二:连接,由图知,所以,又由,恰好是面积的一半,所以是的中点,因此,所以 9.40 【详解】 如图所示,设上的两个点分别为、.连接. 根据面积比例模型,与的面积是相等的,那么与的面积之和,等于与的面 ... ...
~~ 您好,已阅读到文档的结尾了 ~~

