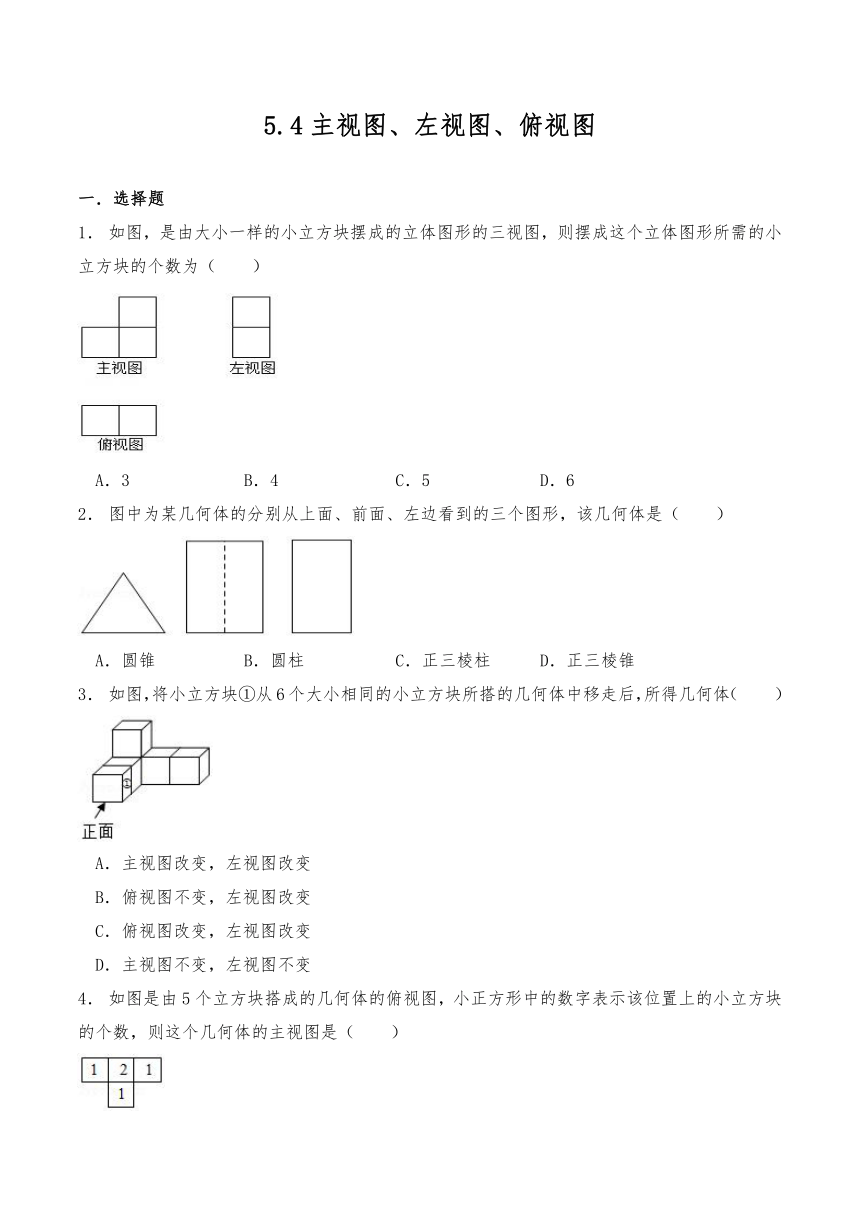
5.4主视图、左视图、俯视图 一.选择题 1. 如图,是由大小一样的小立方块摆成的立体图形的三视图,则摆成这个立体图形所需的小立方块的个数为( ) A.3 B.4 C.5 D.6 2. 图中为某几何体的分别从上面、前面、左边看到的三个图形,该几何体是( ) A.圆锥 B.圆柱 C.正三棱柱 D.正三棱锥 3. 如图,将小立方块①从6个大小相同的小立方块所搭的几何体中移走后,所得几何体( ) A.主视图改变,左视图改变 B.俯视图不变,左视图改变 C.俯视图改变,左视图改变 D.主视图不变,左视图不变 4. 如图是由5个立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上的小立方块的个数,则这个几何体的主视图是( ) A. B. C. D. 5. 如图,是一个几何体的三视图,则这个几何体是( ) A. B. C. D. 6. 在一张桌子上摆放着一些碟子,从3个方向看到的3种视图如图所示,则这个桌子上的碟子共有( ) A.4个 B.8个 C.12个 D.17个 7. 一个几何体由大小相同的小立方块搭成,它的俯视图如图所示,其中小正方形中的数字表示在该位置小立方块的个数,则该几何体的主视图为( ) A. B. C. D. 8. 一个长方体的三视图及相应的棱长如图所示,则这个长方体的体积为( ) A.15 B.30 C.45 D.62 9. 如图所示的主视图和俯视图,其对应的几何体(阴影所示如图)可以是下列( ) A. B. C. D. 10.如图是一个几何体的俯视图,则这个几何体的形状可能是( ) A. B. C. D. 11.如图是由五个棱长为2的小立方块搭建而成的几何体,则它的左视图的面积是( ) A.3 B.4 C.12 D.16 12.如图是某零件的模型,则它的左视图为( ) A. B. C. D. 13.用小立方块搭成的几何体,从正面和上面看的形状图如图,则组成这样的几何体需要立方块个数为( ) A.最多需要8块,最少需要6块 B.最多需要9块,最少需要6块 C.最多需要8块,最少需要7块 D.最多需要9块,最少需要7块 14.下面四个几何体中,同一几何体从前往后看和从上往下看,看到的图形形状相同的共有( )几何体. A.1个 B.2个 C.3个 D.4个 15.下列几何体的主视图与左视图不相同的是( ) A. B. C. D. 16.图①是五棱柱形状的几何体,则它的三视图为( ) A. B. C. D. 二.填空题 17.由一些大小相同的小正方体搭成的几何体从正面和从左面看到的图形如图,则搭成这个几何体的小正方体的个数最多为 ,最少为 . 18.几个完全相同的小正方体搭成如图的几何体,从上面拿掉一个或者几个小正方体(不能直接拿掉被压在下面的小正方体)而不改变几何体的三视图的方法有 种. 19.如图所示的几何体中,主视图与左视图都是长方形的是 . 20.由m个相同的正方体组成一个立体图形,如图的图形分别是从正面和上面看它得到的平面图形,设m能取到的最大值是a,则多项式2a2﹣5a+a2+4a﹣3a2﹣2的值是 . 21.由n个相同的小正方体堆成的几何体,其视图如下所示,则n的最大值是 . 22.如图是一个多面体的表面展开图,如果面F在前面,从左面看是面B,那么从上面看是面 .(填字母,注意:字母只能在多面体外表面出现) 23.一件商品的包装盒是一个长方体(如图1),它的宽和高相等.小明将四个这样的包装盒放入一个长方体大纸箱中,从上面看所得图形如图2所示,大纸箱底面长方形未被覆盖的部分用阴影表示.接着小明将这四个包装盒又换了一种摆放方式,从上面看所得图形如图3所示,大纸箱底面未被覆盖的部分也用阴影表示. 设图1中商品包装盒的宽为a,则商品包装盒的长为 ,图2中阴影部分的周长与图3中阴影部分的周长的差为 (都用含a的式子表示). 24.如图是实心零件的二种 ... ...
~~ 您好,已阅读到文档的结尾了 ~~

