人教版四年级上册数学 平行四边形和梯形的 整理和复习教学设计

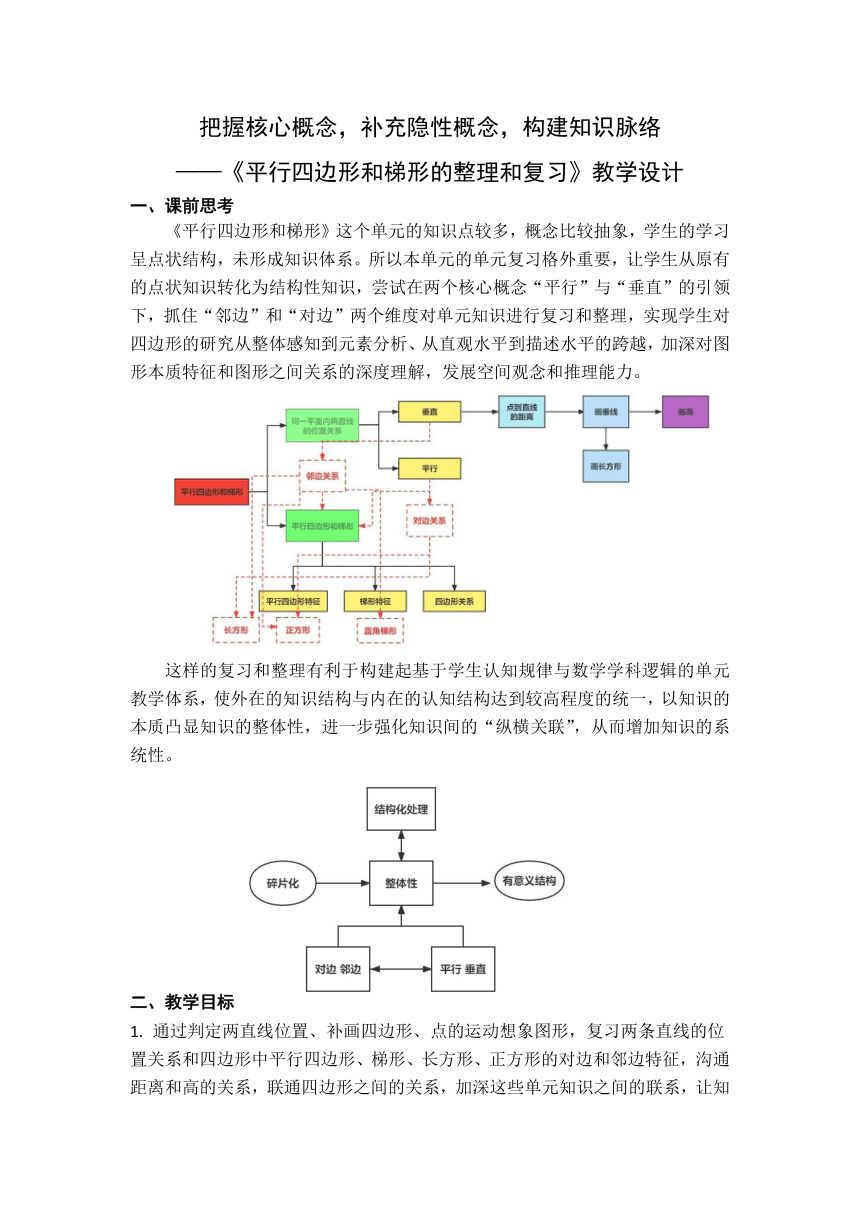
把握核心概念，补充隐性概念，构建知识脉络 ———《平行四边形和梯形的整理和复习》教学设计 课前思考 《平行四边形和梯形》这个单元的知识点较多，概念比较抽象，学生的学习呈点状结构，未形成知识体系。所以本单元的单元复习格外重要，让学生从原有的点状知识转化为结构性知识，尝试在两个核心概念“平行”与“垂直”的引领下，抓住“邻边”和“对边”两个维度对单元知识进行复习和整理，实现学生对四边形的研究从整体感知到元素分析、从直观水平到描述水平的跨越，加深对图形本质特征和图形之间关系的深度理解，发展空间观念和推理能力。 这样的复习和整理有利于构建起基于学生认知规律与数学学科逻辑的单元教学体系，使外在的知识结构与内在的认知结构达到较高程度的统一，以知识的本质凸显知识的整体性，进一步强化知识间的“纵横关联”，从而增加知识的系统性。 二、教学目标 通过判定两直线位置、补画四边形、点的运动想象图形，复习两条直线的位置关系和四边形中平行四边形、梯形、长方形、正方形的对边和邻边特征，沟通距离和高的关系，联通四边形之间的关系，加深这些单元知识之间的联系，让知识结构化形成网络知识图。 2.通过分类归纳，有序整理，系统复习的学习方法，提高学习能力。 3.渗透生活中处处有数学，事物之间有联系可以转化的观念，促进学生的发展观念，提高应用能力。 三、教学重点：整理完善知识结构，发现知识内在的联系，正确解决问题。 四、教学难点：理解图形间的邻边对边内在联系 五、教学过程 （一）抓住核心概念，提升对平行的认知水平 同学们，今天我们学习平行四边形和梯形的复习和整理（揭题） 关于这个单元，我们学习了哪些知识？ 根据学生回答板书。（同一平面内两直线的位置关系 四边形 高） 出示（无格子图） 师：这里有6组直线，为了大家判断更准确，我们可以请格子图来帮忙。 师：哪几组你能一眼就判定位置关系？ 生：2号相交 4号相交 3号垂直（相交的特殊） 生：1号平行 师：怎么判定？ 生：平行线间的距离处处相等 （板书：不相交 平行） 师：5号平行，6号呢？看来格子图也无法帮忙判定。 5.在学习单上有6号这组直线，用你的办法验证平行。 a b 生方法一：画两条垂线段 测量长度 长度相等 生方法二：画一条a的垂线段，也垂直于b 那么a∥b 小结：看来，判断两条直线平行有两个办法，一种是画两条垂线段测量长度，另一种是画一条直线的垂线段，看是否也垂直于另一条直线。 小结：同一平面内两条直线的位置关系一种是不相交就是平行，另一种是相交，而相交中的一种特殊是垂直。 以平行垂直为抓手，补充“对边”“邻边”概念 1.如果上面6组是四边形中的两条边，你们再补上四边形的另外两条边，并说一说你画的是什么图形。 2.反馈：生汇报图形 师：哪些图形跟你画的不一样？（2号 3号） 师：为什么1号4号5号6号画的相同？2号3号不一样？ 生：1.4.5.6号4个点定老了，图形不会变，2.3号还有一个点没有定，图形可以变。 师：1.4.5.6号告诉我们两条边是相对的，这样的边我们叫做一组对边，2.3号告诉我们两条边是相邻的，这样的边我们叫做一组邻边。（板书：对边 邻边） 小结：已知对边关系，四个点就确定了，图形也就确定了。而已知邻边关系，3个点确定了，图形无法确定。 （三）邻边和对边为联结点，整体建构四边形关系 1.根据学生汇报形成上图。 师：①④⑤⑥都是一组平行的对边，那么另一组对边平行吗？ 生：梯形只有一组对边平行，平行四边形和长方形正方形是两组对边都平行。 小结梯形和平行四边形的概念。（板书：只有一组对边平行 两组对边分别平行） 师：两组对边分别平行的四边形是平行四边形，那为什么长方形和正方形也在这里呢？ 生：它们是特殊的平行四边形。 师：特殊在什么地 ... ...