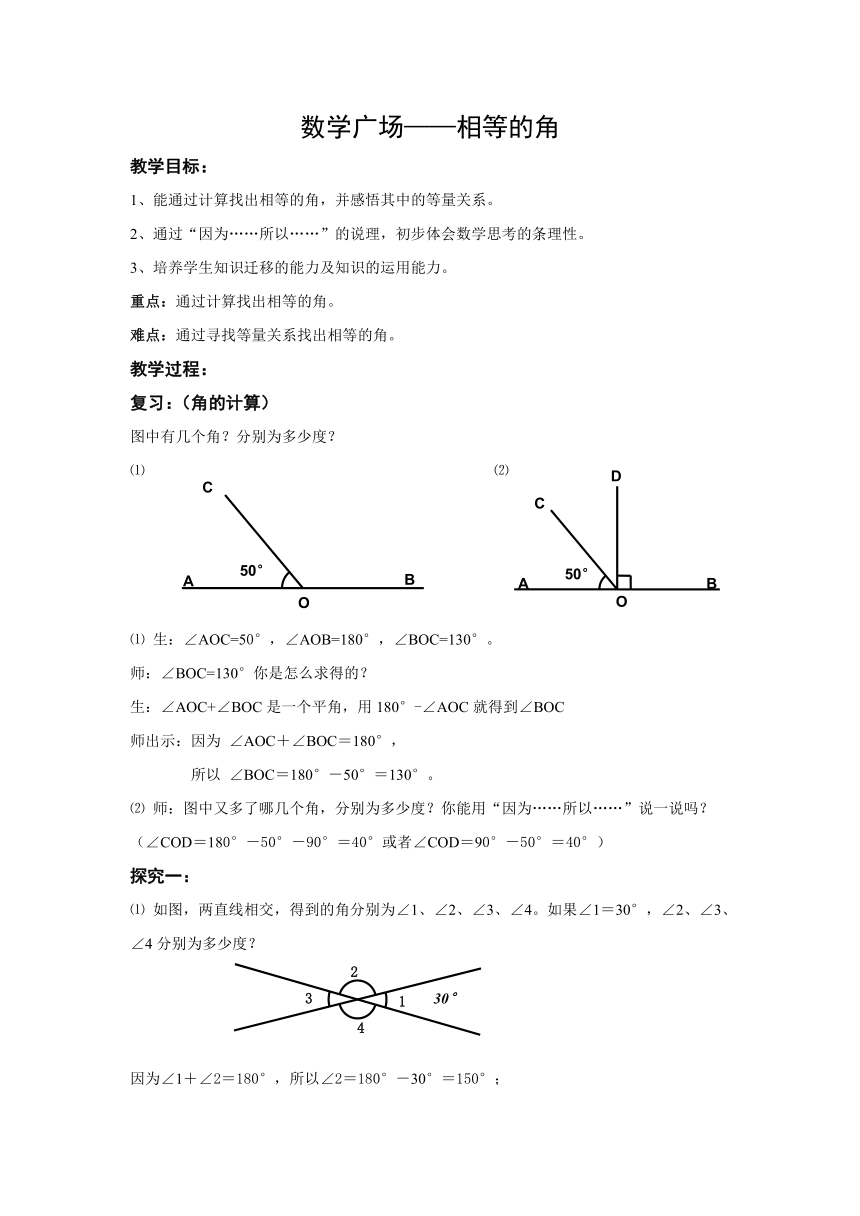
数学广场———相等的角 教学目标: 1、能通过计算找出相等的角,并感悟其中的等量关系。 2、通过“因为……所以……”的说理,初步体会数学思考的条理性。 3、培养学生知识迁移的能力及知识的运用能力。 重点:通过计算找出相等的角。 难点:通过寻找等量关系找出相等的角。 教学过程: 复习:(角的计算) 图中有几个角?分别为多少度? ⑴ ⑵ ⑴ 生:∠AOC=50°,∠AOB=180°,∠BOC=130°。 师:∠BOC=130°你是怎么求得的? 生:∠AOC+∠BOC是一个平角,用180°-∠AOC就得到∠BOC 师出示:因为 ∠AOC+∠BOC=180°, 所以 ∠BOC=180°-50°=130°。 ⑵ 师:图中又多了哪几个角,分别为多少度?你能用“因为……所以……”说一说吗? (∠COD=180°-50°-90°=40°或者∠COD=90°-50°=40°) 探究一: ⑴ 如图,两直线相交,得到的角分别为∠1、∠2、∠3、∠4。如果∠1=30°,∠2、∠3、∠4分别为多少度? 因为∠1+∠2=180°,所以∠2=180°-30°=150°; (请学生口头回答,并出示答案,∠3、∠4的计算请学生书写于练习纸。) 因为∠2+∠3=180°,所以∠3=180°-150°=30°; 因为∠3+∠4=180°,所以∠4=180°-30°=150°。 (∠4也可同过∠1计算求得结果;∠3通过∠4计算求得结果。) 通过计算得出:∠1=∠3=30° ∠2=∠4=150° ⑵ 当∠1=40°时,∠1和∠3还相等吗? 生:相等(不相等)。 师:那么,我们就来通过计算来检验一下,∠1与∠3是否相等。(直接写出得数) ⑶ ∠1和∠3还相等吗?(4题任意选择2题) ① ② ③ ④ 生:第4题缺少条件,无法计算。 师:是的,这题由于缺少条件我们无法计算,我们先将它放在一边。 汇报前3题答案 ………… 师:第4题由于缺少条件,我们无法计算出各个角的大小,请你猜一猜,∠1与∠3相等吗?为什么? 生:∠1=∠3。这两个角加上∠2(∠4)都是180° 师出示:∠1+∠2=180°(点击题号②出现) ∠1+∠4=180°(点击题号④出现) ∠3+∠2=180° ∠3+∠4=180° 师:因此,∠1和∠3都可以通过180°-∠2(∠4)求得。 小结:两个角与同一个角相加,所得结果都是平角,那么(这两个角相等)。 师:除了∠1与∠3相等之外,还有没有相等的角? 生:∠2=∠4,它们加上∠1(∠3)都是平角。 探究二: ⑴ 如下图所示,两个正方形的一个顶点重合,∠1与∠3相等吗? 生:∠1=∠3,因为∠1+∠2=90°,∠3+∠2=90°。 ⑵ 还有哪些相等的角?(增添∠4、∠5) 师:还有哪些相等的角?请说明理由。 小结:两个角与同一个角相加,如果所得结果都是直角,那么(这两个角相等)。 探究三: 师:刚才两个角与同一个角相加,所得的结果都很巧,都是一些特殊的角:平角、直角,如果所得的结果是锐角,或者钝角,那么这两个角还相等吗? 出示问题:两个角与同一个角相加,如果所得结果都是钝角,那么这两个角相等吗? 生:相等;不相等;可能相等,可能不相等。 (这里可以追问,一定相等吗?或者一定不等吗?) 师:老师任意的画了3组角,我们来看看到底相等不相等。 ① ② ∠1+∠2=100° ∠1+∠2=140° ∠3+∠2=160° ∠3+∠2=140° ③ ∠1+∠2=150° ∠3+∠2=150° 生:第①题∠1与∠3相等,第②、③两题∠1与∠3不相等。 师:老师将这些角的实际度数测量了一下,让我们看看是不是这样。 出示∠1、∠2、∠3实际度数。 师:现在我们已经知道两个角与同一个角相加,如果所得结果都是钝角,这两个角不一定相等。那么什么情况下这两个角会相等? 生:所得结果都是相等的钝角时。 小结:两个角与同一个角相加,如果所得结果是相等的钝角,那么这两个角相等。 师:利用刚才的结论请你判断一下∠1与∠3相等吗? ④ ∠1+∠2=160° ∠1+∠2=110° 生:∠1与∠3不 ... ...
~~ 您好,已阅读到文档的结尾了 ~~

