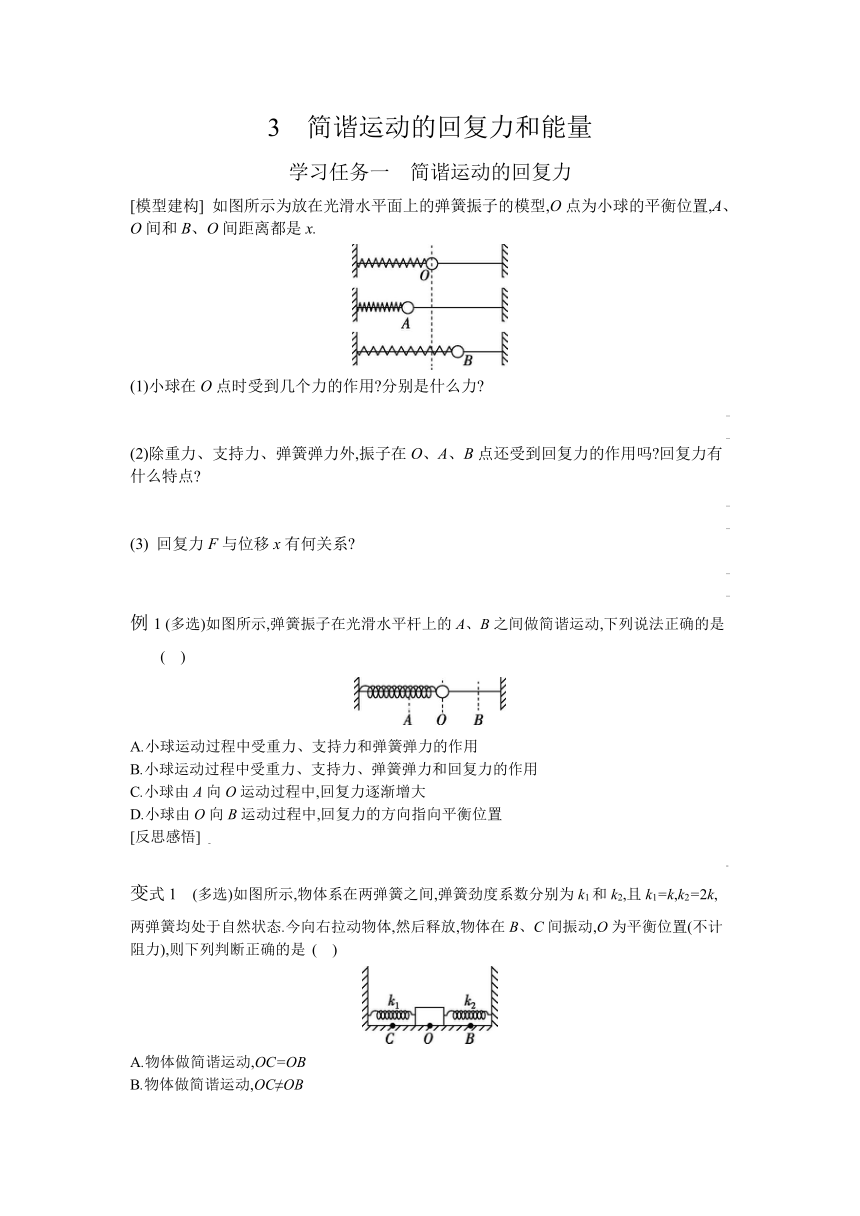
3 简谐运动的回复力和能量 学习任务一 简谐运动的回复力 [模型建构] 如图所示为放在光滑水平面上的弹簧振子的模型,O点为小球的平衡位置,A、O间和B、O间距离都是x. (1)小球在O点时受到几个力的作用 分别是什么力 (2)除重力、支持力、弹簧弹力外,振子在O、A、B点还受到回复力的作用吗 回复力有什么特点 (3) 回复力F与位移x有何关系 例1 (多选)如图所示,弹簧振子在光滑水平杆上的A、B之间做简谐运动,下列说法正确的是 ( ) A.小球运动过程中受重力、支持力和弹簧弹力的作用 B.小球运动过程中受重力、支持力、弹簧弹力和回复力的作用 C.小球由A向O运动过程中,回复力逐渐增大 D.小球由O向B运动过程中,回复力的方向指向平衡位置 [反思感悟] 变式1 (多选)如图所示,物体系在两弹簧之间,弹簧劲度系数分别为k1和k2,且k1=k,k2=2k,两弹簧均处于自然状态.今向右拉动物体,然后释放,物体在B、C间振动,O为平衡位置(不计阻力),则下列判断正确的是 ( ) A.物体做简谐运动,OC=OB B.物体做简谐运动,OC≠OB C.回复力F=-kx D.回复力F=-3kx 例2 一质量为m、底面积为S的正方体木块放在水面上静止(平衡),如图所示.现用力向下将其压入水中一段深度后(未全部浸没)撤掉外力,木块在水面上下振动,试判断木块的振动是否为简谐运动. [反思感悟] 【要点总结】 1.回复力 (1)回复力的方向总是指向平衡位置,回复力为零的位置就是平衡位置. (2)回复力的性质:回复力是根据力的效果命名的,可能由合力、某个力或某个力的分力提供.它一定等于振动物体在振动方向上所受的合力,分析物体受力时不能再加上回复力. 2.简谐运动的动力学特征 回复力F=-kx. (1)k是比例系数,并非弹簧的劲度系数(水平弹簧振子中k为弹簧的劲度系数).k由振动系统决定,与振幅无关. (2)“-”表示回复力的方向与偏离平衡位置的位移方向相反. (3)判断一个物体是否做简谐运动,可找出回复力F与位移x之间的关系,若满足F=-kx,则物体做简谐运动,否则就不做简谐运动. 3.简谐运动的加速度 由F=-kx及牛顿第二定律F=ma,可得a=-x,加速度a与位移x的大小成正比,方向与位移方向相反. 学习任务二 简谐运动的能量 [科学思维] 1.在弹簧振子振动的一个周期内,动能和势能要完成两次周期性变化.经过平衡位置时,动能最大,势能最小(为零);经过最大位移处时,势能最大,动能最小(为零). 2.简谐运动中各物理量的变化规律 小球以O为平衡位置在A、B之间做简谐运动,各物理量的变化规律如下: 位移 回复力 加速度 速度 动能 势能 从O到A 增大 增大 增大 减小 减小 增大 A 最大 最大 最大 0 0 最大 从A到O 减小 减小 减小 增大 增大 减小 O 0 0 0 最大 最大 0 从O到B 增大 增大 增大 减小 减小 增大 B 最大 最大 最大 0 0 最大 从B到O 减小 减小 减小 增大 增大 减小 例3 [2022·缙云中学月考] 如图所示,轻质弹簧下面悬挂一物块组成一个沿竖直方向振动的弹簧振子,弹簧的上端固定于天花板上.当物块处于静止状态时,取它的重力势能为零.现将物块向下拉一小段距离后放手,此后物块在平衡位置附近上下做简谐运动,不计空气阻力,则 ( ) A.物块速度最大时,振动系统的势能为零 B.物块速度最大时,物块的重力势能与弹簧的弹性势能相等 C.物块经过平衡位置时,振动系统的势能最小 D.物块振动过程中,振动系统的机械能不守恒 变式2 图为某个弹簧振子做简谐运动的振动图像,由图像可知 ( ) A.在t=0.1 s时,由于位移为零,所以振动能量为零 B.在t=0.2 s时,弹簧振子的势能最大 C.在t=0.35 s时,弹簧振子具有的能量尚未达到最大值 D.在t=0.4 s时,弹簧振子的动能最大 变式3 [2022·黄岩中学月考] 如图所示,一轻弹簧与质量为m的物体组成弹簧振子,物体在同一条竖直线上的A、B间做简谐运动,O为平衡位置,C为AO的中点,已知OC=h,弹簧的劲度系数为k,某时刻物体恰好以 ... ...
~~ 您好,已阅读到文档的结尾了 ~~