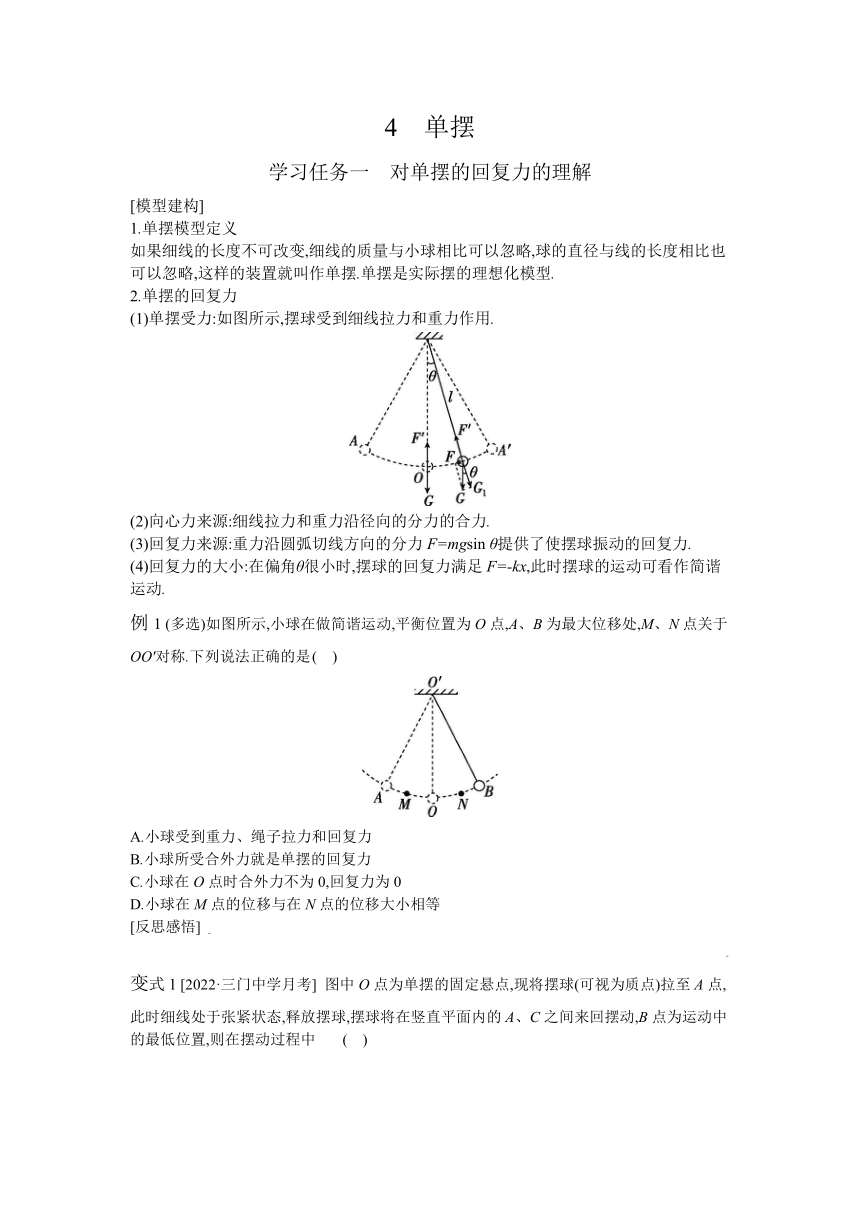
4 单摆 学习任务一 对单摆的回复力的理解 [模型建构] 1.单摆模型定义 如果细线的长度不可改变,细线的质量与小球相比可以忽略,球的直径与线的长度相比也可以忽略,这样的装置就叫作单摆.单摆是实际摆的理想化模型. 2.单摆的回复力 (1)单摆受力:如图所示,摆球受到细线拉力和重力作用. (2)向心力来源:细线拉力和重力沿径向的分力的合力. (3)回复力来源:重力沿圆弧切线方向的分力F=mgsin θ提供了使摆球振动的回复力. (4)回复力的大小:在偏角θ很小时,摆球的回复力满足F=-kx,此时摆球的运动可看作简谐运动. 例1 (多选)如图所示,小球在做简谐运动,平衡位置为O点,A、B为最大位移处,M、N点关于OO'对称.下列说法正确的是 ( ) A.小球受到重力、绳子拉力和回复力 B.小球所受合外力就是单摆的回复力 C.小球在O点时合外力不为0,回复力为0 D.小球在M点的位移与在N点的位移大小相等 [反思感悟] 变式1 [2022·三门中学月考] 图中O点为单摆的固定悬点,现将摆球(可视为质点)拉至A点,此时细线处于张紧状态,释放摆球,摆球将在竖直平面内的A、C之间来回摆动,B点为运动中的最低位置,则在摆动过程中 ( ) A.摆球受到重力、拉力、向心力、回复力四个力的作用 B.摆球在A点和C点处,速度为零,合力与回复力也为零 C.摆球在B点处,速度最大,细线拉力也最大 D.摆球在B点处,速度最大,回复力也最大 学习任务二 单摆的周期、频率与振幅 [科学思维] 单摆周期公式的理解 (1)周期公式的成立条件:当单摆做偏角很小的振动时,才有T=2π,与单摆的振幅及摆球的质量无关,只与摆长l及单摆所在处的重力加速度g有关. (2)对摆长l的理解:摆长为悬点到物体重心的距离. (3)影响g的主要因素:公式中的g由单摆所在的空间位置决定. 例2 一个摆长为2 m的单摆在地球上某地振动时,测得完成100次全振动所用的时间为 284 s. (1)求当地的重力加速度g的大小. (2)把该单摆拿到月球上去,已知月球上的重力加速度是1.60 m/s2,则该单摆的振动周期是多少 变式2 (多选)[2022·黄岩中学月考]如图甲是一个单摆振动的情形,O是它的平衡位置,B、C是摆球所能到达的最远位置,设摆球向右运动为正方向,图乙是这个单摆的振动图像,由此可知 ( ) A.单摆振动的频率是1.25 Hz B.t=0时摆球位于B点 C.t=0.2 s时摆球位于平衡位置O,加速度为零 D.若当地的重力加速度g=π2,则这个单摆的摆长是0.16 m 变式3 (多选)[2022·鲁迅中学期中]如图为同一实验中甲、乙两个单摆的振动图像,从图像可知 ( ) A.两摆球的质量相等 B.两单摆的振幅相等 C.两单摆相位相差 D.两单摆的摆长相等 1.(单摆及其回复力)(多选)关于甲、乙图对应的说法正确的是 ( ) A.图甲是研究弹簧振子的运动实验图,弹簧振子在弹簧弹力作用下做匀变速直线运动 B.图甲是研究弹簧振子的运动实验图,弹簧振子的加速度方向永远指向平衡位置O点 C.图乙是研究单摆的回复力实验图,单摆的回复力是摆球重力和细线拉力的合力 D.图乙中单摆的摆球运动到O点时所受合力不为零 2.(单摆的周期公式)若单摆的摆长不变,摆球的质量减小,摆球离开平衡位置的最大摆角减小,则单摆振动的 ( ) A.频率不变,振幅不变 B.频率不变,振幅改变 C.频率改变,振幅不变 D.频率改变,振幅改变 3.(单摆的周期公式)(多选) 如图所示为甲、乙两单摆的振动图像.下列说法正确的是 ( ) A.若甲、乙两单摆在同一地点摆动,则甲、乙两单摆的摆长之比l甲∶l乙=2∶1 B.若甲、乙两单摆在同一地点摆动,则甲、乙两单摆的摆长之比l甲∶l乙=4∶1 C.若甲、乙两单摆摆长相同,且在不同的星球上摆动,则甲、乙两单摆所在星球的重力加速度之比g甲∶g乙=4∶1 D.若甲、乙两单摆摆长相同,且在不同的星球上摆动,则甲、乙两单摆所在星球的重力加速度之比g甲∶g乙=1∶4 4.(单摆的周期公式)[2022·鲁迅中学月考] 有一单摆,其摆 ... ...
~~ 您好,已阅读到文档的结尾了 ~~