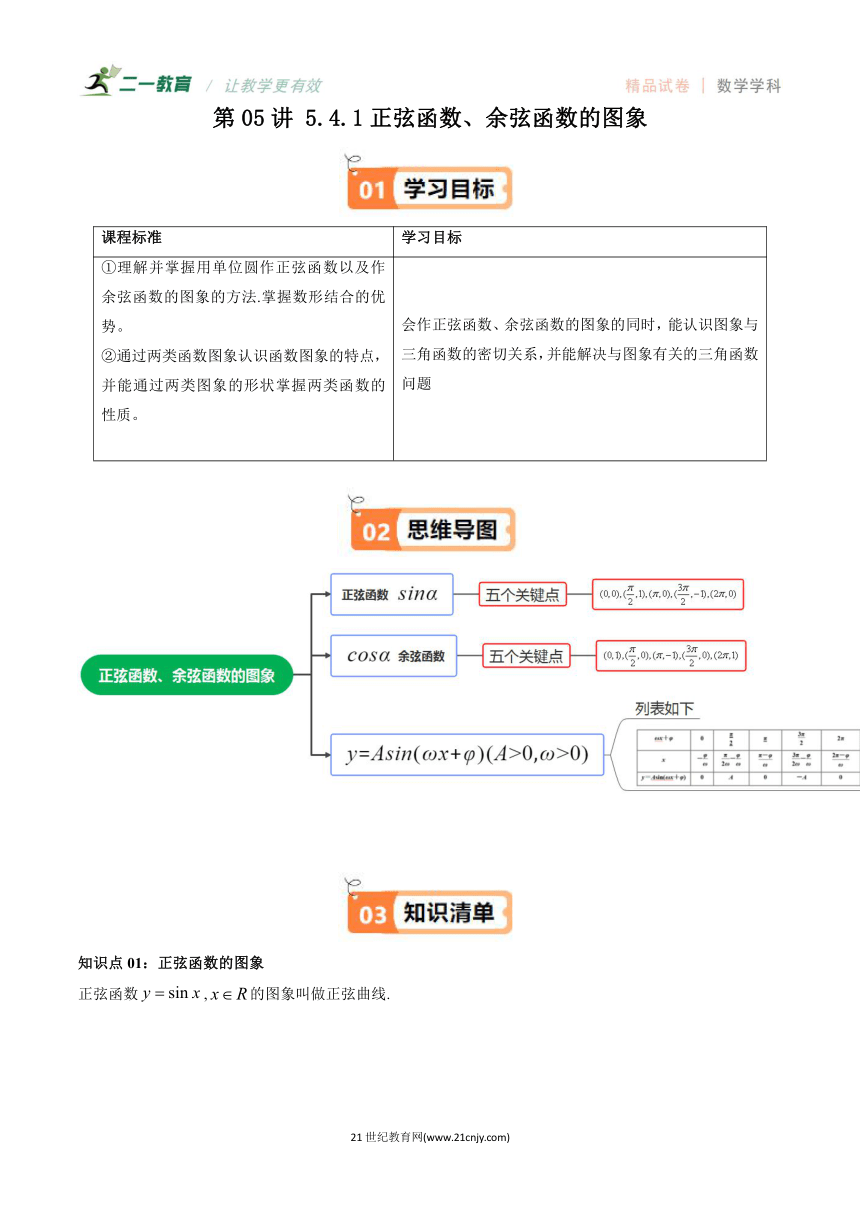
第05讲 5.4.1正弦函数、余弦函数的图象 课程标准 学习目标 ①理解并掌握用单位圆作正弦函数以及作余弦函数的图象的方法.掌握数形结合的优势。 ②通过两类函数图象认识函数图象的特点,并能通过两类图象的形状掌握两类函数的性质。 会作正弦函数、余弦函数的图象的同时,能认识图象与三角函数的密切关系,并能解决与图象有关的三角函数问题 知识点01:正弦函数的图象 正弦函数,的图象叫做正弦曲线. 知识点02:正弦函数图象的画法 (1)几何法: ①在单位圆上,将点绕着点旋转弧度至点,根据正弦函数的定义,点的纵坐标.由此,以为横坐标,为纵坐标画点,即得到函数图象上的点. ②将函数,的图象不断向左、向右平行移动(每次移动个单位长度). (2)“五点法”: 在函数,的图象上,以下五个点: ,,,, 在确定图象形状时起关键作用.描出这五个点,函数,的图象形状就基本确定了.因此,在精确度要求不高时,常先找出这五个关键点,再用光滑的曲线将它们连接起来,得到正弦函数的简图. 【即学即练1】(24-25高一上·上海·课前预习)利用“五点法”作函数,的图象. 知识点03:余弦函数的图象 余弦函数,的图象叫做余弦曲线. 知识点04:余弦函数图象的画法 (1)要得到,的图象,只需把,的图象向左平移个单位长度即可,这是因为. (2)用“五点法”:画余弦函数在上的图象时,所取的五个关键点分别为,,,,再用光滑的曲线连接起来. 【即学即练2】(2024高三·全国·专题练习)已知函数.完成下面表格,并用“五点法”作函数在上的简图: x 0 π 2π 题型01 用“五点法”作三角函数的图象 【典例1】(24-25高一上·上海·课前预习)“五点法”作的图象的步骤: (1)列表(填写下表). 0 x y (2)描点,五个点分别是 , , , , . (3)连线. 【典例2】(23-24高一下·广西梧州·阶段练习)已知函数 (1)请用“五点法”画出函数在一个周期上的图象(先在所给的表格中填上所需的数字,再画图); 0 x 【变式1】(23-24高一下·江西景德镇·期中)已知函数 (1)用“五点法”在所给的直角坐标系中画出函数在区间内的图像并求它在上的增区间; 【变式2】(23-24高一下·四川自贡·期中)已知函数. (1)请用“五点法”画出函数在一个周期上的图象; 题型02 利用图象解三角不等式 【典例1】(23-24高三上·内蒙古通辽·阶段练习)在内,使成立的的取值范围为( ) A. B. C. D. 【典例2】(24-25高一上·上海·课后作业)在内,不等式的解集是 . 【典例3】(23-24高一下·上海嘉定·期中)不等式的解集为 . 【变式1】(2024高一·全国·课后作业)在(0,2π)内使sin x>|cos x|的x的取值范围是( ) A. B. C. D. 【变式2】(23-24高一·全国·课堂例题)不等式的解集为 . 【变式3】(23-24高一下·江西南昌·阶段练习)函数的定义域为 . 题型03 利用图象求方程的解或函数零点的个数问题 【典例1】(2024·陕西榆林·模拟预测)方程在内实数根的个数为( ) A.11 B.10 C.9 D.8 【典例2】(23-24高一下·四川成都·期末)已知函数和,则这两个函数图象在的交点个数为( ) A. B. C. D. 【典例3】(多选)23-24高一下·广东茂名·期中)函数的图像与直线(为常数)的交点可能有( ) A.0个 B.1个 C.2个 D.3个 【典例4】(24-25高一·上海·随堂练习)方程的实数解的个数为 . 【变式1】(24-25高一上·全国·单元测试)方程的实数根的个数为( ) A.4 B.5 C.6 D.7 【变式2】(24-25高一上·全国·课后作业)函数的图象与直线交点的个数是( ) A.0 B.1 C.2 D.3 【变式3】(2024·江苏盐城·模拟预测)函数与的图象的交点个数是( ) A.2 B.3 C.4 D.6 题型04 利用图象根据方程的解或函数零点求参数或零点代数和 【典例1】(2024·内蒙古包头 ... ...
~~ 您好,已阅读到文档的结尾了 ~~