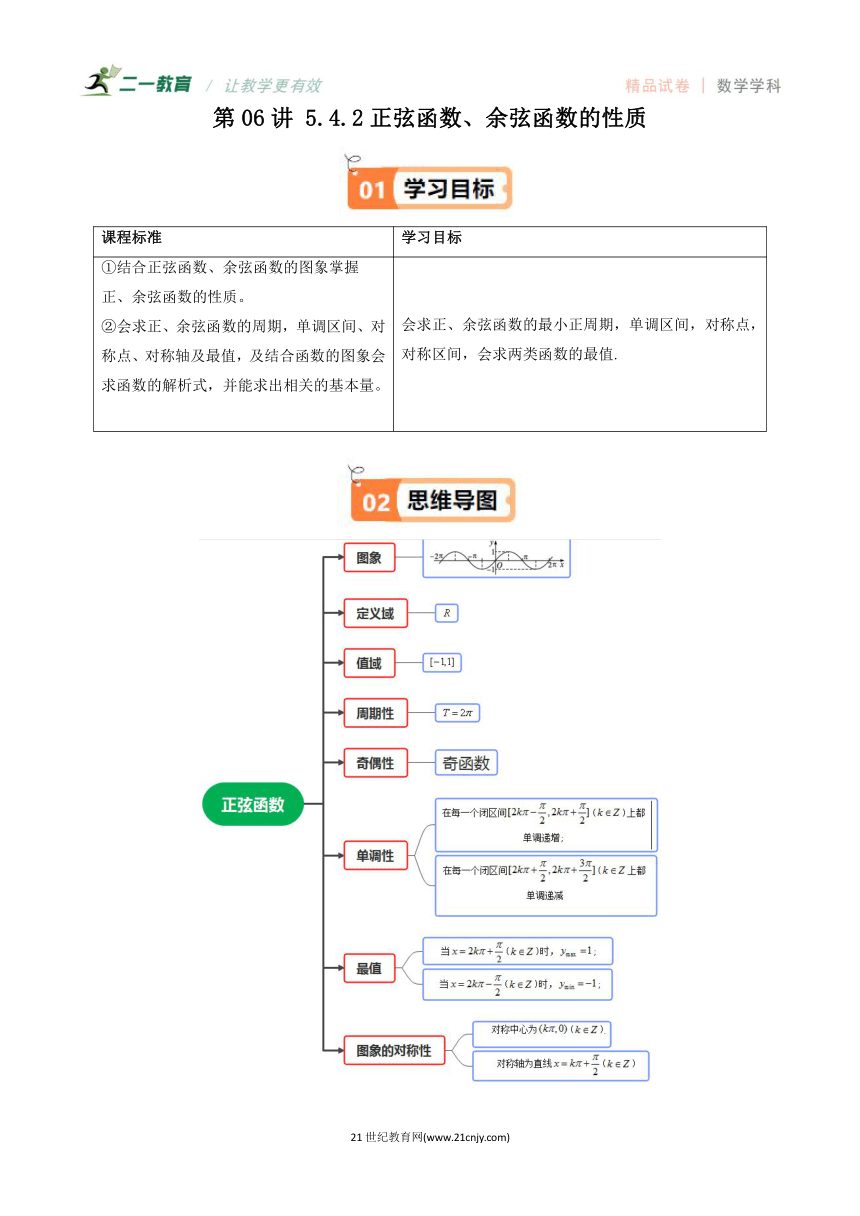
第06讲 5.4.2正弦函数、余弦函数的性质 课程标准 学习目标 ①结合正弦函数、余弦函数的图象掌握 正、余弦函数的性质。 ②会求正、余弦函数的周期,单调区间、对称点、对称轴及最值,及结合函数的图象会求函数的解析式,并能求出相关的基本量。 会求正、余弦函数的最小正周期,单调区间,对称点,对称区间,会求两类函数的最值. 知识点01:函数的周期性 1.周期函数的定义 一般地,设函数的定义域为,如果存在一个非零常数,使得对每一个,都有,且,那么函数就叫做周期函数.非零常数叫做这个函数的周期. 2.最小正周期的定义 如果在周期函数f(x)的所有周期中存在一个最小的正数,那么这个最小正数就叫做的最小正周期. 知识点02:正弦函数、余弦函数的周期性和奇偶性 函数 奇偶性 奇函数 偶函数 当时,为奇函数; 当时,为偶函数; 当时,为奇函数; 当时,为偶函数; 【即学即练1】(24-25高一上·全国·课堂例题)判断下列函数的奇偶性. (1); (2); (3). 知识点03:正弦、余弦型函数的常用周期 函数 最小正周期 或() 或 或() 无周期 【即学即练2】(24-25高一上·全国·课堂例题)求下列三角函数的周期. (1),; (2),; (3),. 知识点04:正弦函数、余弦函数的图象和性质 函数 图象 定义域 定义域 值域 周期性 奇偶性 奇函数 偶函数 单调性 在每一个闭区间()上都单调递增;在每一个闭区间(上都单调递减 在每一个闭区间 ()上都单调递增;在每一个闭区间()上都单调递减 最值 当()时,; 当()时,; 当()时,; 当()时,; 图象的对称性 对称中心为(), 对称轴为直线() 对称中心为(), 对称轴为直线() 【即学即练3】(24-25高一上·全国·课后作业)下列各点中,可以作为函数图象的对称中心的是( ) A. B. C. D. 题型01 三角函数的周期问题及简单应用 【典例1】(24-25高一上·全国·课后作业)下列函数中,以为最小正周期的是( ) A. B. C. D. 【典例2】(多选)(24-25高一上·全国·课后作业)(多选)下列函数中周期为π,且为偶函数的是( ) A. B. C. D. 【变式1】(2024高二下·云南·学业考试)函数的最小正周期是( ) A. B. C. D. 【变式2】(23-24高一下·上海·期末)下列四个函数中,以为最小正周期的奇函数是( ) A. B. C. D. 【变式3】(23-24高一上·河北石家庄·期末)函数的最小正周期是 . 题型02三角函数的奇偶性及其应用 【典例1】(23-24高一·上海·课堂例题)判断下列函数的奇偶性,并说明理由: (1); (2); (3); (4). 【典例2】(23-24高一下·上海·期中)已知函数是奇函数,则 . 【变式1】(2024·贵州黔南·二模)若函数为偶函数,则的值可以是( ) A. B. C. D. 【变式2】(多选)(24-25高三上·江苏南通·阶段练习)下列的函数是偶函数的是( ) A. B. C. D. 题型03函数奇偶性与周期性、单调性,对称性的综合问题 【典例1】(23-24高一下·四川内江·期中)已知函数,的最小正周期为,函数图象关于点对称,且满足函数在区间上单调递增,则( ) A. B. C. D. 【典例2】(23-24高一下·陕西渭南·期中)同时具有下列性质:“①对任意,恒成立;②图象关于直线对称;③在上是增函数”的函数可以是( ) A. B. C. D. 【典例3】(多选)(2024·全国·模拟预测)已知函数在上单调,且有,则( ) A.直线是图像的一条对称轴 B.的最小正周期为 C.点是图像的一个对称中心 D. 【变式1】(24-25高一上·全国·课后作业)已知函数,若关于对称,则的一个单调递增区间可以是( ) A. B. C. D. 【变式2】(多选)(23-24高二下·贵州贵阳·阶段练习)设函数,则下列结论错误的是( ) A.的最小正周期为 B.的图象关于直线对称 C.的一个零点为 D.在区间上单调递 ... ...
~~ 您好,已阅读到文档的结尾了 ~~