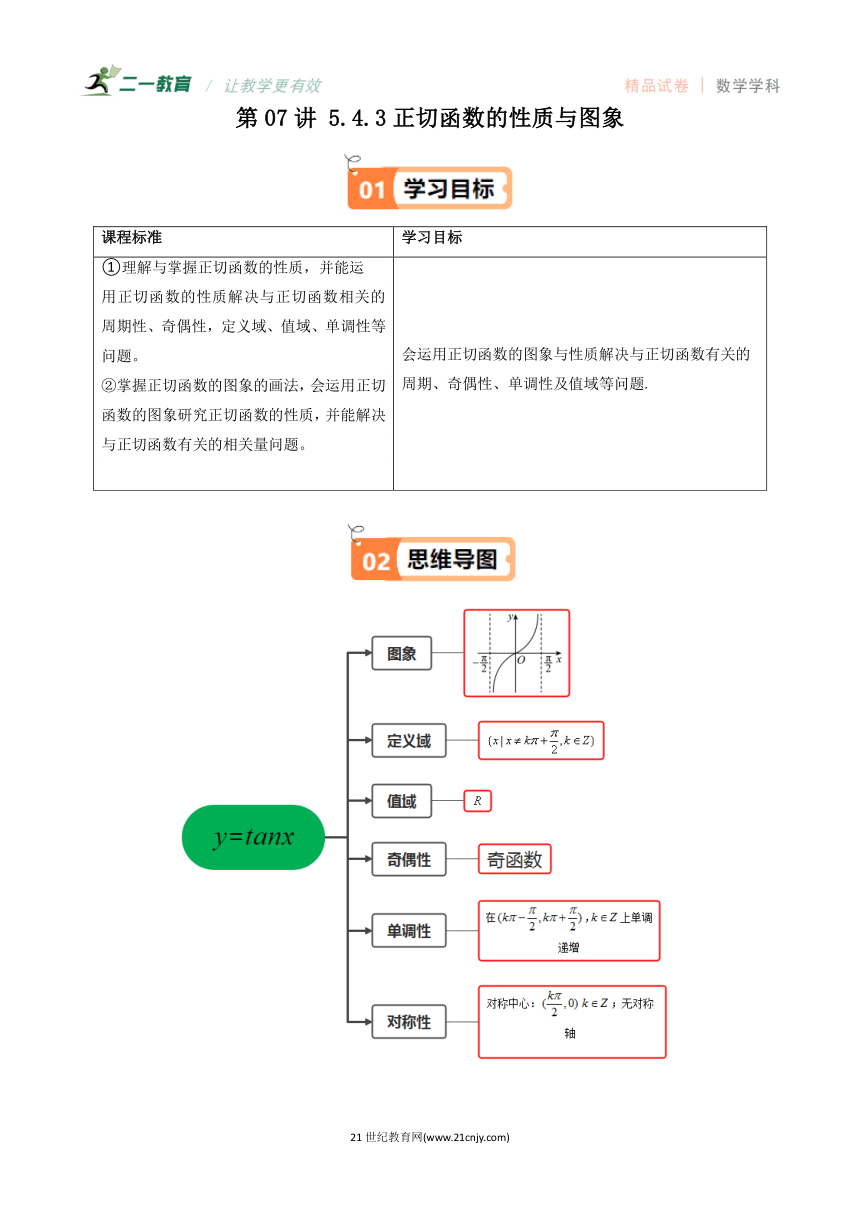
第07讲 5.4.3正切函数的性质与图象 课程标准 学习目标 ①理解与掌握正切函数的性质,并能运 用正切函数的性质解决与正切函数相关的周期性、奇偶性,定义域、值域、单调性等问题。 ②掌握正切函数的图象的画法,会运用正切函数的图象研究正切函数的性质,并能解决与正切函数有关的相关量问题。 会运用正切函数的图象与性质解决与正切函数有关的周期、奇偶性、单调性及值域等问题. 知识点01:正切函数的图象 【即学即练1】(23-24高一上·宁夏银川·期末)函数()的图象可能是( ) A. B. C. D. 知识点02:正切(型)函数的性质 正切函数 正切型函数 定义域 由 值域 周期性 奇偶性 奇函数 当时是奇函数 单调性 在,上单调递增 当,时,由,解出单调增区间 对称性 对称中心:;无对称轴 令:,对称中心为:,无对称轴 【即学即练2】(23-24高一下·陕西咸阳·阶段练习)已知函数,则下列说法正确的是( ) A.在定义域内是增函数 B.是奇函数 C.的最小正周期是π D.图像的对称中心是, 题型01 正切函数的定义域 【典例1】(23-24高一上·陕西宝鸡·期末)函数的定义域是( ) A. B. C. D. 【典例2】(23-24高一上·新疆乌鲁木齐·期末)求函数的定义域 . 【变式1】(23-24高一下·上海黄浦·期末)设,若函数的.定义域为,则的值为 . 【变式2】(23-24高一下·陕西渭南·阶段练习)函数的定义域为 . 题型02 正切函数的值域 【典例1】(23-24高一下·江西·阶段练习)函数,的值域为( ) A. B. C. D. 【典例2】(24-25高一上·上海·随堂练习)已知函数在,上的最小值、最大值分别为1和7,求m和n的值. 【变式1】(23-24高一下·全国·课后作业)函数的值域是( ) A. B. C. D. 【变式2】(23-24高一上·全国·课后作业)函数在x∈[]上的最大值为4,则实数a为 . 题型03求正切函数的单调区间 【典例1】(2024高三·全国·专题练习) 的单调递减区间为 . 【典例2】(24-25高二·上海·假期作业)求下列函数的单调区间: (1) ; (2). 【变式1】(23-24高一·上海·课堂例题)求函数的定义域,并写出其单调区间. 【变式2】(23-24高一上·黑龙江鸡西·期末)求函数的定义域和单调增区间. 题型04 正切函数单调性的应用 【典例1】(24-25高一上·上海·课堂例题)比较与的大小. 【典例2】(24-25高一上·上海·课堂例题)求函数的定义域; 【变式1】(23-24高一上·安徽黄山·期末)已知函数在内是减函数,则的取值范围是 A. B. C. D. 【变式2】(23-24高一下·广西钦州·期中)不等式的解集为( ) A. B. C. D. 【变式3】(多选)(23-24高一下·浙江杭州·开学考试)下列不等式中,正确的是( ). A. B. C. D. 题型05 正切函数的周期性与奇偶性 【典例1】(23-24高一下·广东佛山·期中)函数的最小正周期为( ) A.2 B.1 C. D. 【典例2】(23-24高一下·四川眉山·阶段练习)已知,且,则 【典例3】(23-24高一·上海·课堂例题)判断下列函数的奇偶性,并说明理由: (1); (2); (3); (4). 【变式1】(24-25高一上·上海·随堂练习)若函数()的最小正周期是2,则a的值为 . 【变式2】(23-24高一下·辽宁沈阳·阶段练习)已知, . 【变式3】(23-24高一上·河北邢台·阶段练习)已知函数的图象关于原点中心对称,则的最小值为 . 【变式4】(2024高一·全国·专题练习)判断下列函数的奇偶性: (1); (2). 题型06 正切函数图象的对称性 【典例1】(23-24高一下·河南驻马店·阶段练习)下列是函数的对称中心的是( ) A. B. C. D. 【典例2】(23-24高三上·广西贵港·阶段练习)函数图像的对称轴方程为( ) A. B. C. D. 【变式1】(2024高三·全国·专题练习)函数 的对称中心 ... ...
~~ 您好,已阅读到文档的结尾了 ~~