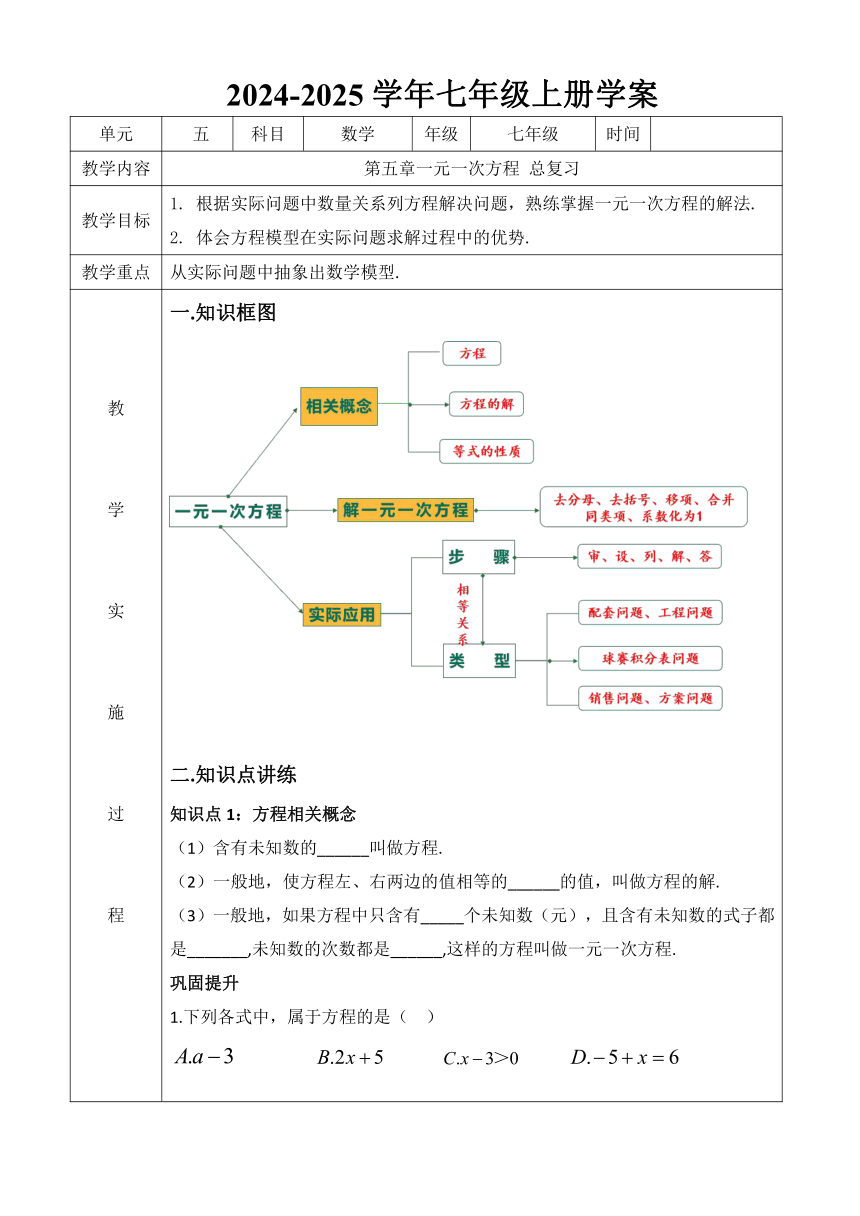
2024-2025学年七年级上册学案 单元 五 科目 数学 年级 七年级 时间 教学内容 第五章一元一次方程 总复习 教学目标 1. 根据实际问题中数量关系列方程解决问题,熟练掌握一元一次方程的解法. 2. 体会方程模型在实际问题求解过程中的优势. 教学重点 从实际问题中抽象出数学模型. 教 学 实 施 过 程 教 学 实 施 过 程 教 学 实 施 过 程 一.知识框图 二.知识点讲练 知识点1:方程相关概念 (1)含有未知数的_____叫做方程. (2)一般地,使方程左、右两边的值相等的_____的值,叫做方程的解. (3)一般地,如果方程中只含有_____个未知数(元),且含有未知数的式子都是_____,未知数的次数都是_____,这样的方程叫做一元一次方程. 巩固提升 1.下列各式中,属于方程的是( ) 若x=2是方程4x+m=6的解,则m的值为_____. 知识点2:等式的性质 等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等. 如果a=b,那么a±c=b±c. 等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等. 如果a=b,那么ac=bc; 巩固提升 1.如果x-y=0,那么根据等式的性质,下列变形错误的是( 已知-4m+3=-4n+3,根据等式的性质,则m_____n. 知识点3:解一元一次方程 (1)解一元一次方程的一般步骤包括:_____、去括号、_____、合并同类项、_____. (2)去分母:一元一次方程中如果有分母,利用等式的性质_____,将方程的两边都乘各分母的_____,从而去掉分母. (3)移项:把等式一边的某项_____移到另一边,叫做移项,其依据是_____. (4)系数化为1:利用等式的性质_____,将方程两边除以未知数的系数,将未知数的系数化为1. 巩固提升 1.解方程-2(3x-1)=x,以下去括号正确的是( ) 2.已知代数式2+x和-x-6的值相等,则x的值为_____. 3.若多项式2a+1和10-a互为相反数,则a的值为_____. 4.解下列方程 (1)-3x+5=6x-7 (2)3(x-2)=2x-1 知识点4:实际问题 (1)用一元一次方程解决实际问题的基本过程包括:设_____、列方程、_____、检验所得结果、确定答案.正确分析问题中的_____关系是列方程的基础. (2)配套问题中的基本相等关系: 若m个A物品与n个B物品配成一套,则_____×A数量=____×B的数量. 工程问题中的基本相等关系: 工作量=_____×工作时间. (4)销售问题中的基本相等关系: 售价=_____+进价=进价×(1+利润率) 利润=_____-进价. 利润率=(利润÷进价)×100%. 巩固提升 1. 某种商品因换季准备打折出售,如果按原定价的七五折出售,将赔25元,而按原定价的九折出售,将赚20元,则这种商品的原价是( ) A.500元 B.400元 C.300元 D.200元 2.某次数学竞赛共有20道题,已知做对一道得4分,做错一道或不做扣1分,某同学最后的得分是55分,则他做对了( ) A.16道 B.15道 C.14道 D.13道 3.一项工程由甲单独完成需要8天,由乙单独完成需要10天.现在由甲先做3天,剩下的甲乙合作完成.若设完成此项工程共需x天,可列方程为_____. 课堂练习 1.下列方程是一元一次方程的是( ) 2.下列方程变形正确的是( ) 3.阅读课上,语文老师将一些书分给各小组,若每个小组分8本,则剩余3本;若每个小组分9本,则缺少2本,问有几个小组?设有x个小组,可列方程为( ) 解下列方程. 5.已知 4a-5=2(x+1)-a与 -2(x+3)=4都是关于x的一元一次方程,且有相同的解,求a的值. 6.一项工程,由甲单独做需要10天完成,乙单独做需要15天完成.若甲先做5天,再由甲乙合作,共完成全部工程的三分之二,则甲乙合作多少天? 学习检测 1.已知关于x的方程2x+k=15的解是x=3,则k的值是( ) A.6 B.9 C.7 D.5 2.某车间有84名工人,平均每人每天加工16个大齿轮或10个小齿轮,已知1个大齿轮和2个小齿轮配套.为使每天加工的大、小齿轮刚好配套,应该 ... ...
~~ 您好,已阅读到文档的结尾了 ~~