2025年中考数学二轮复习专题 解三角形（含答案）

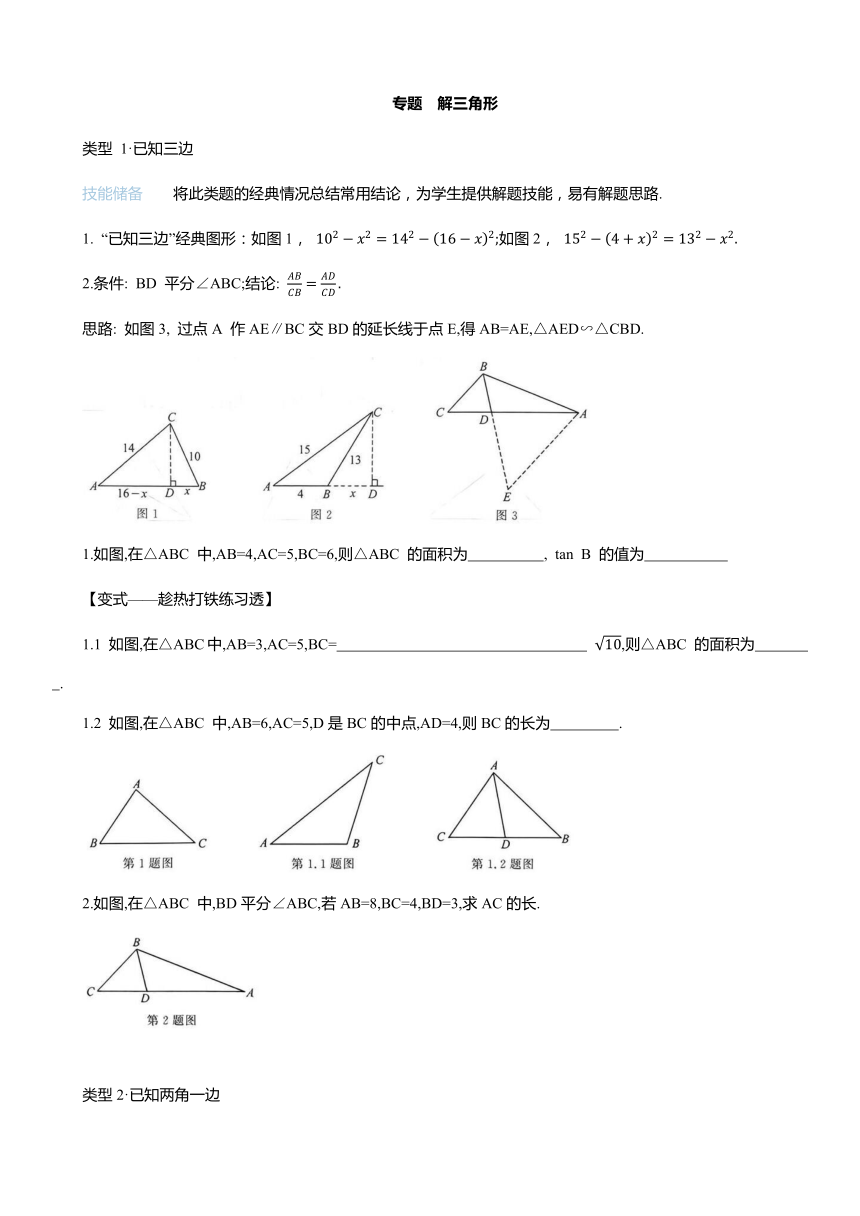
专题 解三角形 类型 1·已知三边 技能储备 将此类题的经典情况总结常用结论，为学生提供解题技能，易有解题思路. 1. “已知三边”经典图形：如图1， 如图2， 2.条件: BD 平分∠ABC;结论: 思路: 如图3, 过点A 作AE∥BC交BD的延长线于点E,得AB=AE,△AED∽△CBD. 1.如图,在△ABC 中,AB=4,AC=5,BC=6,则△ABC 的面积为 , tan B 的值为 【变式———趁热打铁练习透】 1.1 如图,在△ABC中,AB=3,AC=5,BC= ,则△ABC 的面积为 . 1.2 如图,在△ABC 中,AB=6,AC=5,D是BC的中点,AD=4,则BC的长为 . 2.如图,在△ABC 中,BD平分∠ABC,若AB=8,BC=4,BD=3,求AC的长. 类型2·已知两角一边 技能储备 将此类题的经典情况总结常用结论，为学生提供解题技能，易有解题思路. 通常已知特殊角或已知角的锐角三角函数值，需通过转换角或作垂线把特殊角或已知锐角三角函数值的角放在直角三角形中，进而可求边. 3.如图,∠B=45°,BC=14.①若 则 AB 的长为 ;若 tan(∠B+∠C)=7,则AC 的长为 . 4.如图,∠ABC=45°,BD⊥AC,tan∠CBD= ①若 AB =20,则 AD 的长为 ;若AC=5,则 BD 的长为 . 5.如图,在△ABC 中,D 是 AC 的中点.①若 则 AB 的长为 ;若 则AC 的长为 . 6.|每领跑改编| 如图,在△ABC中, CD平分∠BCA,BD=15,求CD 的长. 类型3·已知一边一角(两边)，另两边有数量关系 技能储备 将此类题的经典情况总结常用结论，为学生提供解题技能，易有解题思路. 经典情况举例：在等腰△ABC中，已知底边 BC和一腰AC上的高，可解△ABC. 在△ABD中,已知一边一角(BD, ∠ADB),另两边(AB, AD)有数量关系.如图1, 如图 7.如图,将一张矩形纸片ABCD 沿对角线 AC 折叠,点 B 落在点 E 处,AE 交 DC 边于点 F,已知 ，则折叠后重叠部分的面积为 . 8.如图,在矩形OABC 中,AB=2,BC=6,将矩形OABC 折叠使得点 C 与点 A 重合,折痕交 BC于点 D,交 OA 于点 E,点 O 的对应点为点 F,折痕 DE 的长为 . 9.如图,在Rt△ABC中,∠ACB=90°,D是AB 上一点,且2∠BCD=∠A,BC=3,BD=1,则AC的长为 . 10.如图,在 Rt△ABC中,∠C=90°,AD 平分∠BAC,若 ,求 AC 的长. 类型4·已知两边一角 11.如图,在△ABC中,BC=4,AC=3,∠C=60°,则AB 的长为 . 12.如图,在△ABC中,tan∠ABC=2,BD⊥AC,AB= ,BD= 则 BC 的长为 . 13.如图,在△ABC中, D是BC的中点， 则 BC 的长为 . 【变式—趁热打铁练习透】 13.1 如图,在△ABC 中, CD 平分∠ACB,BC=CD=25,则 AC 的长为 . 14.如图,在△ABC中,CD⊥AB,∠ACB=45°,AD=5,BD=12,求CD 的长. 预备专题 解三角形 点拨过点A 作AD⊥BC 于点D,设BD=x,则 1.1. 点拨过点C 作CD⊥AB,交AB 的延长线于点D.设BD=x,则. 1.2. 详解 如图,延长AD 至点F,使 FD=AD,过点B作BE⊥AF 于点E,连接BF. ∴AF=2AD=2×4=8. ∵D是BC的中点,∴CD=BD. 又∠ADC=∠FDB,AD=FD,∴△ADC≌△FDB. ∴AC=FB=5. 设AE=x,则EF=8-x. 在 Rt△ABE 和 Rt△FBE 中, ∵根据勾股定理， 即 解得 ∵在 Rt△BDE中,根据勾股定理、得 详解如图,过点 A 作AE∥BC,交 BD 的延长线于点E,过点 A 作AF⊥BE于点F. ∴∠CBD=∠E,△CBD∽△AED.∴BD=CD=CBE. ∵BD 平分∠ABC,∴∠ABD=∠CBD. ∴∠ABD=∠E.∴AB=AE=8. ∴BE=BD+ED=3+6=9. ∵AB=AE,AF⊥BE,∴BF=EF= ,∠AFD=90°. 在 Rt△ABF 和 Rt△ADF 中,∵根据勾股定理,AF = DF ,即 3.解:①6 点拨过点A 作AD⊥BC 于点 D.设 BD=x,则AD=x,CD=14-x. tanC=14=x= ②10 详解如图,过点C作CE⊥AB,交 BA 的延长线于点 E. ∴∠E=90°,∠EAC=∠B+∠ACB. ∵tan(∠B+∠ACB)=7,∴tan∠EAC=7. ∴在 Rt△AEC中, 即CE=7AE. ∵在 Rt△BEC 中,∠B=45°,BC=14, ∴在 Rt△AEC 中,根据勾股定理,得 ②6详解①如图,过点A 作 AE⊥BC于 点E,交 BD 于点 F.∴∠AEB=∠AEC=90°. ∵BD⊥AC,∴∠BDC=∠BDA=90°. ∵∠BFE=∠AFD, ,即∠CBD=∠EAC. 在 Rt△A ... ...