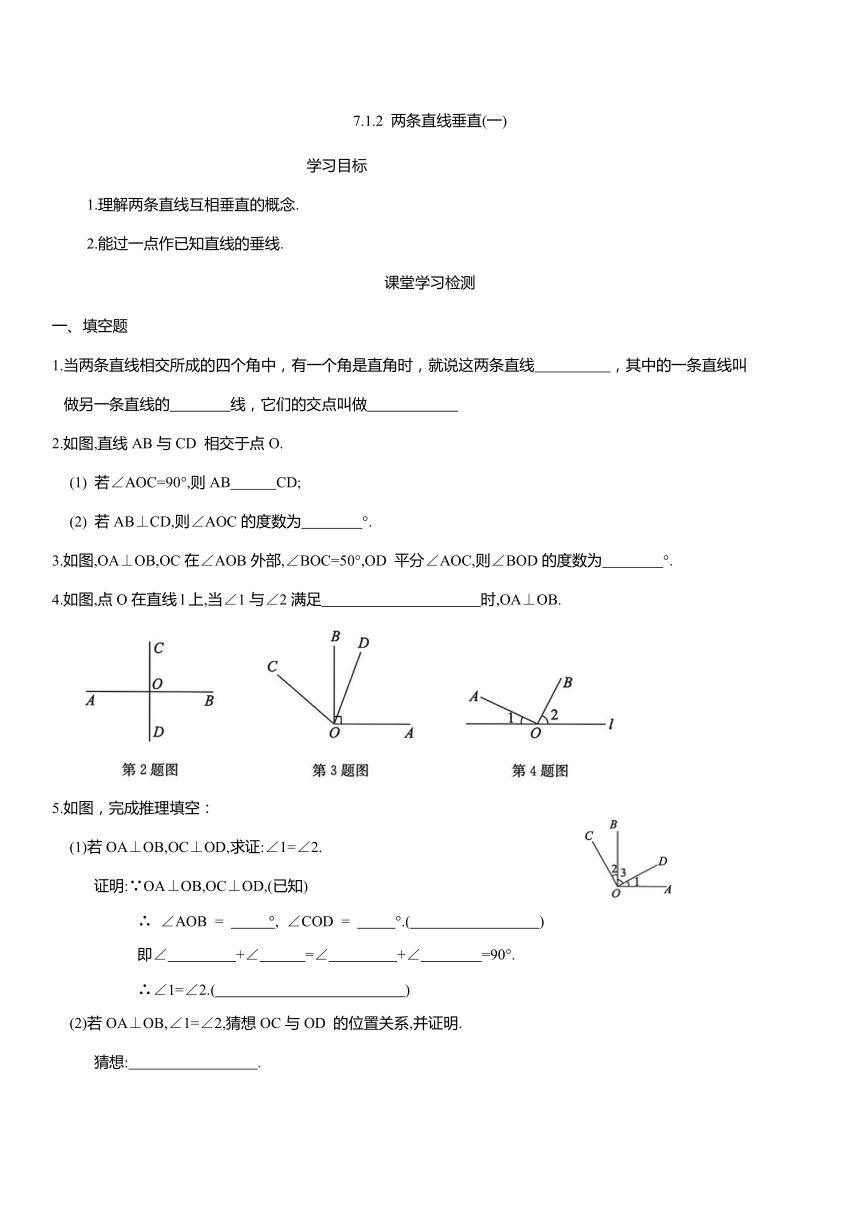
7.1.2 两条直线垂直(一) 学习目标 1.理解两条直线互相垂直的概念. 2.能过一点作已知直线的垂线. 课堂学习检测 一、填空题 1.当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线 ,其中的一条直线叫做另一条直线的 线,它们的交点叫做 2.如图,直线AB与CD 相交于点O. (1) 若∠AOC=90°,则AB CD; (2) 若AB⊥CD,则∠AOC的度数为 °. 3.如图,OA⊥OB,OC在∠AOB外部,∠BOC=50°,OD 平分∠AOC,则∠BOD的度数为 °. 4.如图,点O在直线l上,当∠1与∠2满足 时,OA⊥OB. 5.如图,完成推理填空: (1)若OA⊥OB,OC⊥OD,求证:∠1=∠2. 证明:∵OA⊥OB,OC⊥OD,(已知) ∴ ∠AOB = °, ∠COD = °.( ) 即∠ +∠ =∠ +∠ =90°. ∴∠1=∠2.( ) (2)若OA⊥OB,∠1=∠2,猜想OC与OD 的位置关系,并证明. 猜想: . 证明:∵OA⊥OB,(已知) ∴∠ = °.( ) 即∠ +∠ =90°. ∵∠1=∠2,(已知) ∴∠2+∠3= °.( )即 ∴OC OD.( ) 二、按要求画图 6.如图,已知直线AB,点 P 在直线AB 上,点Q在直线AB 外. (1)过点 P作AB 的垂线CD; (2)过点Q作CD的垂线,垂足为M. ·Q 综合·运用·诊断 一、选择题 7.过直线l外一点P 画l的垂线CD,下列各图中,三角尺操作正确的是( ). 8.如图,OA⊥OC,OB⊥OD,且∠BOC=α,那么∠AOD等于( ). 二、填空题 9.下列说法中正确的有 .(写出全部正确说法的序号) ①在同一平面内,一条直线只有一条垂线; ②两条直线相交,若其中有一组对顶角互补,则这两条直线互相垂直; ③过线段外一点,作这条线段的垂线,垂足一定在线段上; ④在同一平面内,过一点有且只有一条直线与已知直线垂直. 10.如图,直线 BC,DE 相交于点O,OA⊥BC于点O. OM平分∠BOD.如果∠AOE =50°,那么∠BOM 的度数是 °. 三、解答题 11.如图,OA⊥BC于点O,且∠DOC=5∠AOD-12°,求∠BOD的度数. 12.如图,直线 AB,CD 相交于点O,OE⊥CD,垂足为O,OM 平分 (1)求 的度数; (2)在∠AOM的内部画射线ON,使得 ,那么ON是 的平分线吗 请说明理由. 拓展·探究·思考 解答题 13.已知直线( 求∠BOC的度数. 14.如图,直线 AB,CD 相交于点O, OC 平分 且 求 的度数. 练习2 1.互相垂直;垂;垂足. 2.(1)⊥; (2) 90. 3.20. 4.∠1+∠2=90°(∠1和∠2互余). 5.(1)90;90;垂直定义;1;3;2;3;同角的余角相等; (2)OC⊥OD;AOB;90;垂直定义;1;3;90;等量代换;COD;⊥;垂直定义. 6. 图略. 7. D. 8. B. 9.②④. 10.20. 11.解:∵OA⊥BC, ∴∠AOC=∠AOB=90°. 即∠DOC+∠AOD=90°. 又∵∠DOC=5∠AOD-12°, ∴∠AOD=17°. 12.解:(1)∵∠AOC与∠BOD 是对顶角, ∴∠BOD=∠AOC=50°. ∵OE⊥CD, ∴∠DOE=90°. ∴∠BOE=∠BOD+∠DOE=50°+90°=140°. ∵OM 平分∠BOE, (2)ON是∠AOD的平分线.理由如下: ∵∠DOM=20°,∠MON=45°, ∵∠AOC=50°, ∴ON 平分∠AOD,即 ON 是∠AOD 的平分线. 13.30°或150°. 14.解:∵OE⊥OF, ∴∠FOE=90°. 即∠BOF+∠BOE=90°. 又∵∠BOF=2∠BOE, ∴∠BOE=30°. 又∵OC平分∠AOE, ∴∠DOB=∠AOC=75°. ... ...
~~ 您好,已阅读到文档的结尾了 ~~