分析的化身—欧拉 课件 (3)

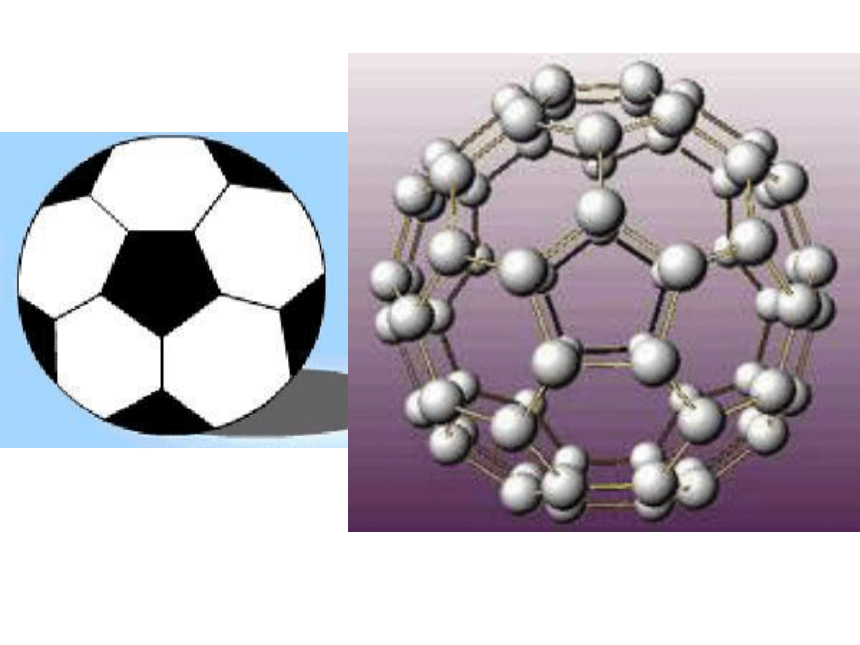
课件14张PPT。数学家欧拉 ? 欧拉，瑞士数学家，欧拉是科学史上最多产的一位杰出的数学家，他从19岁开始发表论文，直到76岁，他一生共写下了886本书籍和论文，其中在世时发表了700多篇论文。彼得堡科学院为了整理他的著作，整整用了47年。在他双目失明后的17年间，也没有停止对数学的研究，口述了好几本书和400余篇的论文。 欧拉对物理力学、天文学、弹道学、航海学、建筑学、音乐都有研究！有许多公式、定理、解法、函数、方程、常数等是以欧拉名字命名的。欧拉写的数学教材在当时一直被当作标准教程。19世纪伟大的数学家高斯曾说过“研究欧拉的著作永远是了解数学的好方法”。欧拉还是数学符号发明者，他创设的许多数学符号，例如π，i，e，sin，cos，tg，Σ，f (x)等等，至今沿用。 多面体欧拉定理的发现 一：复习1、什么叫正多面体 ？ ①每个面都是有相同边数的正多边形； ②每个顶点都有相同数目的棱数。 2、正多面体有哪几种？ 2302012正二十面体2301220正十二面体21286正八面体21268正六面体2644正四面体 V+F-E 棱数E 面数F 顶点数V 正 多 面 体什么样的 多面体符合 V+F-E=2? 考虑一个多面体，例如正六面体，假定它的面是用橡胶薄膜做成的，如果向内部充以气体，那么它会连续（不破裂）变形，最后可变成一个球面。 表面经过连续变形可变为球面的多面体，叫做简单多面体。 我们所学的几何体，如棱柱、棱锥、正多面体 等一切凸多面体都是简单多面体。 简单多面体凸多面体棱柱棱锥正多面体正四面体正方体简单多面体概念： 欧拉定理: 简单多面体的顶点数V、面数F及棱数E间有关系 V+F-E=2 这个公式叫欧拉公式。 欧拉定理的应用 利用欧拉定理可解决一些实际问题例1．一个简单多面体各面都是三角形， 顶点数V=6,求面数F、棱数E .要Face,不要Edge 例2．一个简单多面体的棱数可能是6吗？ 分析：设有简单多面体棱数E=6， 由欧拉公式V+F-E=2得V+F=8 又V≥4，F≥4，所以V+F≥8 所以V=4、F=4，即有4个顶点、4个面。 由于四面体有且只有4个顶点，从面有且只有4个面 所以符合条件的多面体只有一种类型：四面体即三棱锥。 练习：是否有棱数为7的简单多面体？小结:1.正多面体的概念和种类2.简单多面体概念 3.欧拉定理及应用 讨论: C60的分子结构中,正五边形和正六边形各有几个？