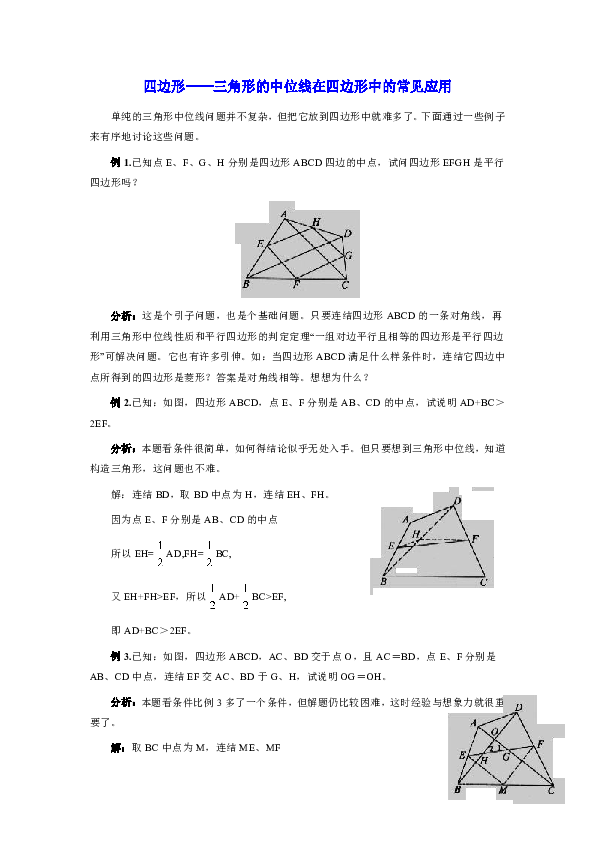
四边形———三角形的中位线在四边形中的常见应用 单纯的三角形中位线问题并不复杂,但把它放到四边形中就难多了。下面通过一些例子来有序地讨论这些问题。 例1.已知点E、F、G、H分别是四边形ABCD四边的中点,试问四边形EFGH是平行四边形吗? 分析:这是个引子问题,也是个基础问题。只要连结四边形ABCD的一条对角线,再利用三角形中位线性质和平行四边形的判定定理“一组对边平行且相等的四边形是平行四边形”可解决问题。它也有许多引伸。如:当四边形ABCD满足什么样条件时,连结它四边中点所得到的四边形是菱形?答案是对角线相等。想想为什么? 例2.已知:如图,四边形ABCD,点E、F分别是AB、CD的中点,试说明AD+BC>2EF。 分析:本题看条件很简单,如何得结论似乎无处入手。但只要想到三角形中位线,知道构造三角形,这问题也不难。 解:连结BD,取BD中点为H,连结EH、FH。 因为点E、F分别是AB、CD的中点 所以EH=AD,FH=BC, 又EH+FH>EF,所以AD+BC>EF, 即AD+BC>2EF。 例3.已知:如图,四边形ABCD,AC、BD交于点O,且AC=BD,点E、F分别是AB、CD中点,连结EF交AC、BD于G、H,试说明OG=OH。 分析:本题看条件比例3多了一个条件,但解题仍比较困难,这时经验与想象力就很重要了。 解:取BC中点为M,连结ME、MF 因为点E、F分别是AB、CD的中点,所以ME=AC,MF=BD, ME∥AC,MF∥BD, 又AC=BD,所以ME=MF, 则∠MEF=∠MFE. 又ME∥AC,MF∥BD,所以∠1=∠MEF,∠2=∠MFE, 所以∠1=∠2,OG=OH. 下面两道题留给同学们思考。 (1)已知:四边形ABCD,点M、N分别是AD、BC的中点,点P、Q分别是AC、BD的中点,且AC=BD,试说明MN⊥PQ。 (2)已知:如图,四边形ABCD,AB=CD,点E、F分别 是AD、BC的中点,BA、CD的延长线交EF的延长线于点 H,试说明∠BGF=∠CHF。 三角形中位线辅助线的应用 三角形的中位线定理是几何中一个重要定理,它不仅反映了图形间线段的位置关系,而且还揭示了线段间的数量关系,利用三角形中位线定理可以解决许多相关的问题. 一、借助中位线定理选择结论 例1如图1,已知四边形ABCD中,R、P分别是BC、CD上的点,E、F分别是AP、RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( ). (A)线段EF的长逐渐增大 (B)线段EF的长逐渐减小 (C)线段EF的长不变 (D)线段EF的长与点P的位置有关 分析:由E,F分别为AP,RP的中点,由此可联想三角形的中位线,故连接AR,由于已知条件可知EF为ARP的中位线,根据中位线定理可知EF=AR, 由于点P从点C到点D移动的移动过程中,AR始终不变,∴EF的长度也不变. 解:连接AR,∵E,F分别是PA,PR的中点,∴EF=AB, ∵AR不变,∴线段EF的长不变.故选(C). 点评:本题通过巧妙地连接AR,把问题转化为三角形中位线问题,借助于中位线的性质俩来解决. 二、借助中位线定理求长度 例2某花木场有一块如四边形ABCD的空地(如图2),两对角线相等,各边的中点分别是E、F、G、H,用篱笆围成的四边形EFGH场地的周长为40cm,则对角线AC= cm 分析:根据E、F分别为BA,BC的中点,可知EF为△ABC的中位线,根据中位线定理可得EF=AC,同理可得HG=AC,HE=BD,FG=BD,根据两对角线相等可得EF=FG=GH=HE,由此可求到EF的长,也就求到AC的长. 解:∵E,F分别是BA,BC的中点,∴EF=AC,同理可得HG=AC, ∵E,H分别是AB,AD的中点,∴EH=BD,同理可得FG=BD, ∵AC=BD,∴EF=FG=GH=HE, ∵EF+FG+GH+HE=40cm,∴EF=10cm, ∴AC=2EF=20cm. 点评:根据已知条件的特点,本题是将四边形问题转化为三角形问题,通过多次利用三角形中位线的性质,确定EF的长,进而求到AC的长. 三、借助中位线定理说理 ... ...
~~ 您好,已阅读到文档的结尾了 ~~