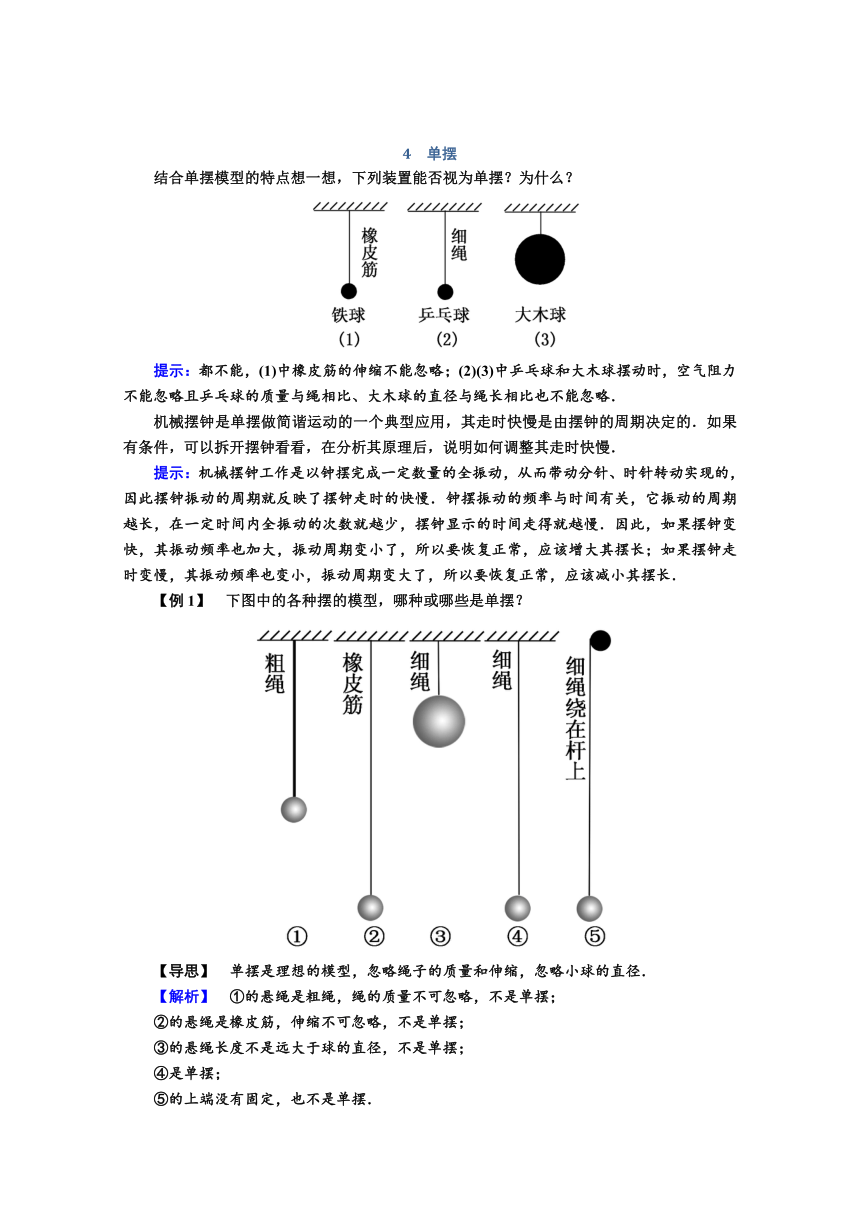
4 单摆 结合单摆模型的特点想一想,下列装置能否视为单摆?为什么? 提示:都不能,(1)中橡皮筋的伸缩不能忽略;(2)(3)中乒乓球和大木球摆动时,空气阻力不能忽略且乒乓球的质量与绳相比、大木球的直径与绳长相比也不能忽略. 机械摆钟是单摆做简谐运动的一个典型应用,其走时快慢是由摆钟的周期决定的.如果有条件,可以拆开摆钟看看,在分析其原理后,说明如何调整其走时快慢. 提示:机械摆钟工作是以钟摆完成一定数量的全振动,从而带动分针、时针转动实现的,因此摆钟振动的周期就反映了摆钟走时的快慢.钟摆振动的频率与时间有关,它振动的周期越长,在一定时间内全振动的次数就越少,摆钟显示的时间走得就越慢.因此,如果摆钟变快,其振动频率也加大,振动周期变小了,所以要恢复正常,应该增大其摆长;如果摆钟走时变慢,其振动频率也变小,振动周期变大了,所以要恢复正常,应该减小其摆长. 【例1】 下图中的各种摆的模型,哪种或哪些是单摆? 【导思】 单摆是理想的模型,忽略绳子的质量和伸缩,忽略小球的直径. 【解析】 ①的悬绳是粗绳,绳的质量不可忽略,不是单摆; ②的悬绳是橡皮筋,伸缩不可忽略,不是单摆; ③的悬绳长度不是远大于球的直径,不是单摆; ④是单摆; ⑤的上端没有固定,也不是单摆. 【答案】 ④是单摆 (多选)单摆是为研究振动而抽象出的理想化模型,其理想化条件是( ABC ) A.摆线质量不计 B.摆线长度不伸缩 C.摆球的直径比摆线长度短得多 D.只要是单摆的运动就是一种简谐运动 解析:单摆由摆线和摆球组成,摆线只计长度不计质量,摆球只计质量不计大小,且摆线不伸缩,A、B、C正确.但把单摆作为简谐运动来处理是有条件的,只有在摆角很小(θ<5°)的情况下才能视单摆运动为简谐运动. 考点二 单摆的回复力 1.单摆的平衡位置 如图所示,摆球静止在O点时,悬线竖直下垂,摆球所受到的重力G与悬线的拉力F′平衡,合力为零,小球保持静止,所以O点是单摆的平衡位置. 2.单摆的回复力 (1)如图所示,摆球运动到某点P时,摆球受重力G和绳子拉力F′两个力作用,将重力沿切向、径向正交分解,则绳子的拉力F′与重力的径向分量G1的合力提供了摆球做圆周运动所需要的向心力,而重力的切向分力F则提供了摆球振动所需要的回复力F=mgsinθ. (2)单摆在摆角很小时做简谐运动 设单摆的摆长为l,在最大偏角θ很小的条件下,摆球对O点的位移x的大小与θ角所对应的弧长、θ角所对应的弦长OP都近似相等,即x==OP, 若摆角θ用弧度表示,则由数学关系知sinθ≈θ==,则重力沿切向的分力F=mgsinθ≈mg, 令k=,则F=kx,因为F的方向与x方向相反,故F=-kx. 由此可见,单摆在摆角很小条件下的振动为简谐运动. 3.单摆的振动图象 我们已经知道,简谐运动的图象是正弦曲线(或余弦曲线),而在偏角很小的情况下,单摆做简谐运动,故它的振动图象也是正弦曲线(或余弦曲线). 4.理解单摆的受力和运动特点 (1)摆球以悬挂点为圆心在竖直平面内沿圆弧做变速圆周运动,做圆周运动需要向心力,向心力由绳子的拉力与重力的径向分量的合力提供. (2)摆球以最低点为平衡位置做振动,做振动需要回复力,回复力由摆球重力的切向分力提供(或者说是由摆球所受合外力沿圆弧切向分力提供). (3)单摆的运动既有圆周运动,又有简谐运动(摆角很小的情况下) ①单摆振动的平衡位置:回复力F为零,而合力不为零,此时合力提供摆球做圆周运动的向心力. ②单摆振动的最大位移处:向心力(F′-G1)为零,而合力不为零,此时合力提供摆球振动的回复力. 【例2】 下列关于单摆的说法,正确的是( ) A.单摆摆球从平衡位置运动到正向最大位移处时的位移为A(A为振幅),从正向最大位移处运动到平衡位置时的位移为-A B ... ...
~~ 您好,已阅读到文档的结尾了 ~~