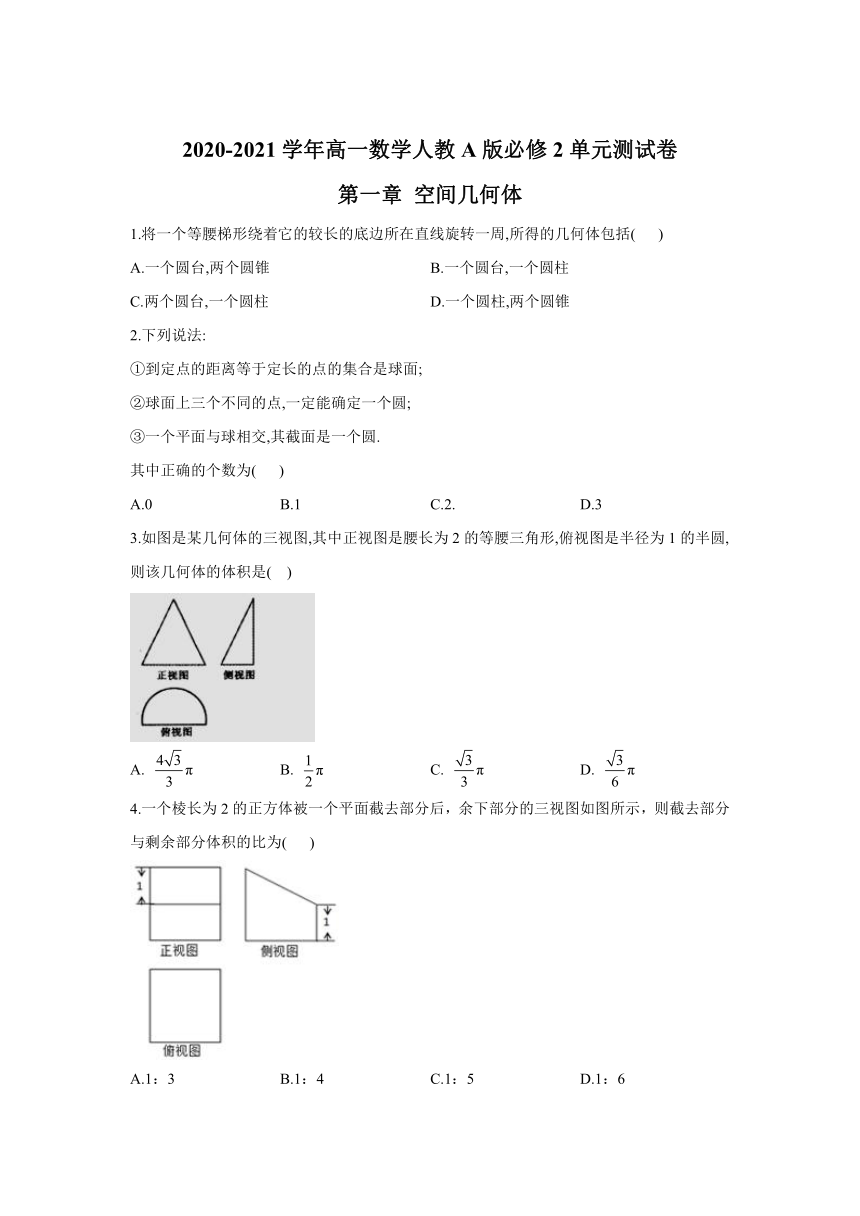
2020-2021学年高中数学人教A版必修2单元测试卷 第一章 空间几何体 Word版含解析

2020-2021学年高一数学人教A版必修2单元测试卷 第一章 空间几何体 1.将一个等腰梯形绕着它的较长的底边所在直线旋转一周,所得的几何体包括( ) A.一个圆台,两个圆锥 B.一个圆台,一个圆柱 C.两个圆台,一个圆柱 D.一个圆柱,两个圆锥 2.下列说法: ①到定点的距离等于定长的点的集合是球面; ②球面上三个不同的点,一定能确定一个圆; ③一个平面与球相交,其截面是一个圆. 其中正确的个数为( ) A.0 B.1 C.2. D.3 3.如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是(?? ) A. B. C. D. 4.一个棱长为2的正方体被一个平面截去部分后，余下部分的三视图如图所示，则截去部分与剩余部分体积的比为( ) A.1：3 B.1：4 C.1：5 D.1：6 5.已知圆柱的上、下底面的中心分别为,过直线的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( ) A. B. C. D. 6.圆台的上、下底面的面积分别为,侧面积为,则这个圆台的体积为( ) A. B. C. D. 7.已知三棱锥中,,则三棱锥的体积是( ) A.4 B.6 C. D. 8.如图,矩形是水平放置的一个平面图形的直观图,其中,则原图形是（ ） A.正方形????????????????????????B.矩形 C.菱形????????????????????????? D.一般的平行四边形 9.如图，矩形是水平放置的一个平面图形的直观图，其中，，则原图形是( ) A.正方形 B.矩形 C.菱形 D.一般的平行四边形 10.一个三角形用斜二测画法画出来的直观图是边长为2的正三角形,则原三角形的面积是( ) A. B. C. D. 都不对 11.已知圆台的上下底面半径分别是2,5,且侧面面积等于两底面面积之和,则该圆台的母线长为_____. 12.某几何体的三视图如图所示,则该几何体的体积为_____,该几何体最长棱的长度为_____. 13.已知某几何体的三视图如图所示,则该几何体的表面积为_____体积为_____. 14.在棱长为2的正方体,中,分别为棱,的中点,点在线段上,则三棱锥的体积为_____. 15.已知某几何体的正视图、侧视图都是等腰三角形,俯视图是矩形,尺寸如图所示. 1.说明该几何体的结构特征; 2.求该几何体的体积; 3.求该几何体的全面积. 答案以及解析 1.答案：D 解析：设等腰梯形较长的底边为,则绕着底边所在直线旋转一周可得一个圆柱和两个圆锥(轴截面如图D-8-11).故选D. 2.答案：C 解析：①②都对.③中一个平面与球相交,其截面是一个圆面,而不是圆. 3.答案：D 解析：由三视图, 可知给定的几何体是一个圆锥的一半,故所求的体积为. 4.答案：A 解析：由题意可知：几何体被平面平面分为上下两部分， 设：正方体的棱长为2,上部棱柱的体积为：； 下部为：. 截去部分与剩余部分体积的比为：1:3. 故选：A. 5.答案：C 解析：设圆柱的底面半径为,高为,由题意得,所以,所以圆柱的表面积为.故选C. 6.答案：A 解析：，∴， ，∴，∴. ∴. 故答案为：. 7.答案：C 解析：由,得.由,得,则,得,又,所以平面.所以三棱锥的体积为. 8.答案：C 解析：本题考查斜二测画法的逆用 根据斜二测的画法可得,还原出的图如下, 其中 (平行于轴的长度不变). (平行于轴的长度扩为2倍).由于,且, 所以为平行四边形,又,所以为菱形.故答案为 C. 9.答案：C 解析：根据题意，直观图的两组对边分别平行且. 还原为平面图形是邻边不垂直，且，如图所示， ， 四边形是菱形. 故选：C. 10.答案：A 解析：∵三角形在其直观图中对应一个边长为2正三角形, ∴直观图的面积是 由斜二测画法中直观图和原图的面积的关系, ∴原三角形的面积为, 11.答案： 12.答案：; 解析：由几何体的三视图可知该几何体为如图所示的正方体中的三棱锥, 其中正方体的棱长为2,C所在棱的中点,所以该几何体的体积为,因为都是直角三角形,所以只需比较的长度,易知,所以该几何体中最长的棱为,其长度为 13.答案：; 解析：由三视图还原该 ... ...