数学必修2测试卷Word含答案

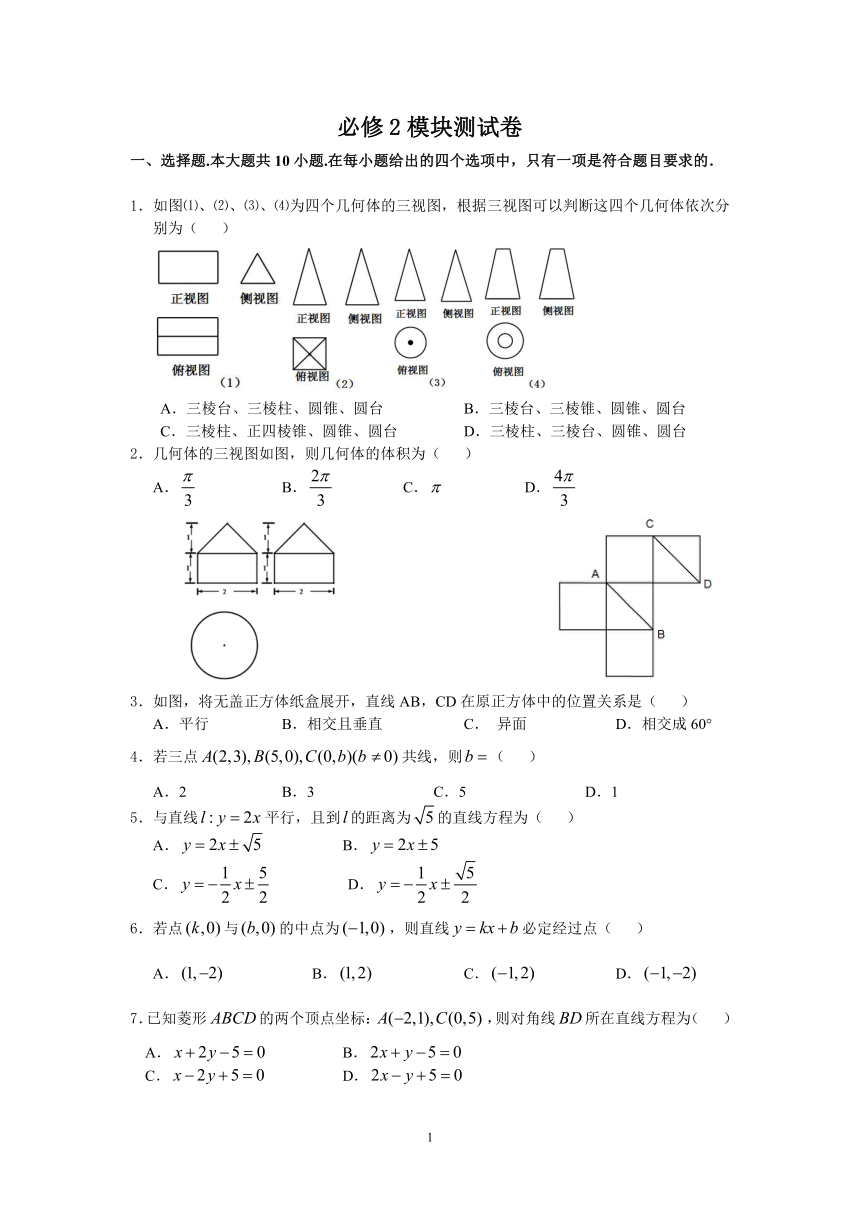
必修2模块测试卷 一、选择题.本大题共10小题.在每小题给出的四个选项中，只有一项是符合题目要求的． 1．如图⑴、⑵、⑶、⑷为四个几何体的三视图，根据三视图可以判断这四个几何体依次分别为（ ） A．三棱台、三棱柱、圆锥、圆台 B．三棱台、三棱锥、圆锥、圆台 C．三棱柱、正四棱锥、圆锥、圆台 D．三棱柱、三棱台、圆锥、圆台 2．几何体的三视图如图，则几何体的体积为（ ） A． B． C． D． 3．如图，将无盖正方体纸盒展开，直线AB，CD在原正方体中的位置关系是（ ） A．平行 B．相交且垂直 C． 异面 D．相交成60° 4．若三点共线，则（ ） A．2 B．3 C．5 D．1 5．与直线平行，且到的距离为的直线方程为（ ） A． B． C． D． 6．若点与的中点为，则直线必定经过点（ ） A． B． C． D． 7．已知菱形的两个顶点坐标：，则对角线所在直线方程为（ ） A． B． C． D． 8. 一个长方体，其正视图面积为，侧视图面积为，俯视图面积为，则长方体的对角线长为（ ） A． B． C．6 D． 9．圆心为且与直线相切的圆的方程是（ ） A． B． C． D． 10．由直线上的一点向圆引切线，则切线长的最小值为（ ） A．1 B． C． D．3 二、填空题：本大题共4小题． 11. 直线与直线垂直，则＝ . 12．已知正四棱台的上下底面边长分别为2，4，高为2，则其斜高为 . 13．一个水平放置的平面图形，其斜二测直观图是一个等腰梯形，其底角为，腰和上底均为1. 如图，则平面图形的实际面积为 . 14.设集合，.当时，则正数的取值范围 . 三、解答题：本大题共6小题．解答须写出文字说明、证明过程和演算步骤． 15．如图，在平面直角坐标系中，已知平行四边形的三个顶点坐标：． ⑴ 求边所在直线的方程（结果写成一般式）； ⑵ 证明平行四边形为矩形，并求其面积． 16. 如图，四棱锥P－ABCD的底面ABCD是平行四边形，M、N分别是AB、PC的中点，且.证明：平面PAD⊥平面PDC. 17. 如图，已知直线，直线以及上一点．求圆心在上且与直线相切于点的圆的方程． 18. 已知正四棱锥P－ABCD如图. ⑴ 若其正视图是一个边长分别为的等腰三角形，求其表面积S、体积V； ⑵ 设AB中点为M，PC中点为N，证明：MN//平面PAD. 19．在棱长为2的正方体中，设是棱的中点. ⑴ 求证：； ⑵ 求证：平面；⑶．求三棱锥的体积. 20．已知圆和直线． ⑴ 证明：不论取何值，直线和圆总相交； ⑵ 当取何值时，圆被直线截得的弦长最短？并求最短的弦的长度． 必修2模块测试卷参考答案 一、选择题.本大题共10小题.在每小题给出的四个选项中，只有一项是符合题目要求的． 1． C 2． D 3． D 4． C 5． B 6． A 7． A 8． D 9． A 10．C 二、填空题：本大题共4小题． 11. 0或2 12． 13． 14. 三、解答题：本大题共6小题．解答须写出文字说明、证明过程和演算步骤． 15．【解】⑴. 过两点的直线的斜率，，∴， 又因直线过点，∴所在直线的方程为：，即. ⑵. 可求，故矩形的面积. 16. 【证明】设PD中点为H，连接NH、AH，则NH是三角形PCD的中位线，， 而，故，四边形AMNH为平行四边形，. 而，故，又， 故平面PCD，而，故平面PCD， 平面PAD，故平面PAD⊥平面PDC. 17. 【解】设圆心为，半径为，依题意，. 设直线的斜率，过两点的直线斜率，因，故， ∴，解得.. 所求圆的方程为. 18. 【解】⑴. 设CD中点为E，则正四棱锥的正视图为三角形PME. 依题意，， 故几何体的表面积S＝， 体积V＝. ⑵. 设PD中点为F，连接NF，AF. 则NF为三角形PCD的中位线，故， ，故，四边形MNFA为平行四边形， ，平面PAD，平面PAD，故MN//平面PAD. 19． 【证明】连接BD，AE. 因四边形ABCD为正方形，故， 因底面ABCD，面ABCD，故，又， 故平面，平面，故. ⑵. 连接，设，连接， 则为中点，而为的中点，故为三角形的中位线， ，平面，平 ... ...