暑期特训：图形变换（3）

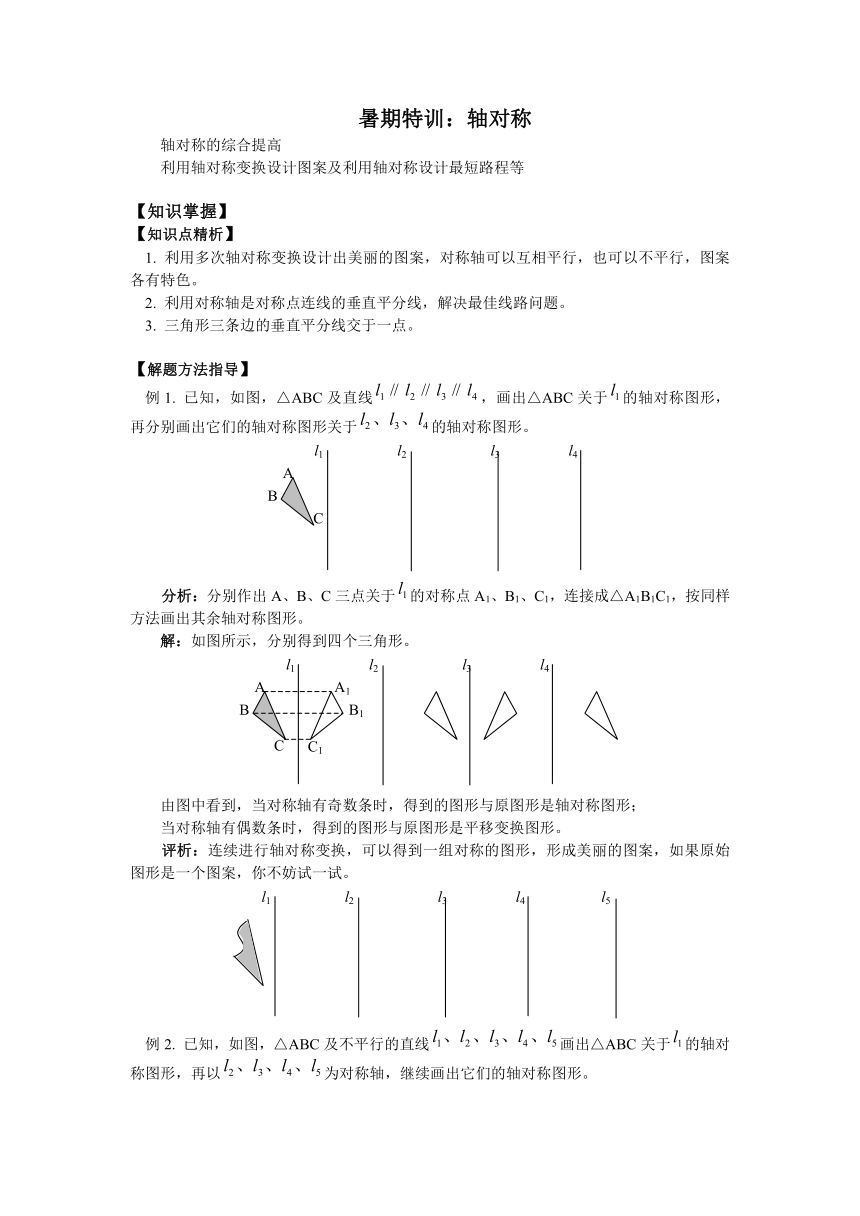
暑期特训：轴对称 轴对称的综合提高 利用轴对称变换设计图案及利用轴对称设计最短路程等 【知识掌握】 【知识点精析】 1. 利用多次轴对称变换设计出美丽的图案，对称轴可以互相平行，也可以不平行，图案各有特色。 2. 利用对称轴是对称点连线的垂直平分线，解决最佳线路问题。 3. 三角形三条边的垂直平分线交于一点。 【解题方法指导】 例1. 已知，如图，△ABC及直线，画出△ABC关于的轴对称图形，再分别画出它们的轴对称图形关于的轴对称图形。 分析：分别作出A、B、C三点关于的对称点A1、B1、C1，连接成△A1B1C1，按同样方法画出其余轴对称图形。 解：如图所示，分别得到四个三角形。 由图中看到，当对称轴有奇数条时，得到的图形与原图形是轴对称图形； 当对称轴有偶数条时，得到的图形与原图形是平移变换图形。 评析：连续进行轴对称变换，可以得到一组对称的图形，形成美丽的图案，如果原始图形是一个图案，你不妨试一试。 例2. 已知，如图，△ABC及不平行的直线画出△ABC关于的轴对称图形，再以为对称轴，继续画出它们的轴对称图形。 分析：画法同例1类似，图案成放射状。 解：如图所示，分别得到五个三角形 评析：例1、例2画图的方法虽然类似，但由于对称轴不一样，所以得到的图形不一样，如果原始图形是一个图案，你不妨试一试。 【考点突破】 【考点指要】 轴对称图形在实际中应用很广泛，但在中考时，由于时间的限制，不可能设计很复杂的图形，常常给出图形，让考生判断它是不是轴对称图形，有时，也给出网格，让考生设计一个图形，并且面积等于某一个数值，这类问题尽可能设计成三角形或特殊的四边形，便于计算面积。 有关线段垂直平分线的题目虽然常出现在考题中，但难度很大的题目却不常见。 【典型例题分析】 例1. 已知，如图，△ABC中，AB的垂直平分线与BC的垂直平分线交于O点，求证：AC的垂直平分线也经过O点。 分析：由l1是AB的垂直平分线，O是l1上一点，连结OA、OB，则OA＝OB；同样连结OC，则OB＝OC，于是得到OA＝OC，可知O也在AC的垂直平分线l3上。 证明：∵O在AB的垂直平分线l1上，O也在BC的垂直平分线l2上 连结OA、OB、OC ∴OA＝OB，OB＝OC（线段的垂直平分线上一点，到线段两端的距离相等） ∴OA＝OC ∴O在AC的垂直平分线l3上（到线段的两端距离相等的点，在这条线段的垂直平分线上） 即AC的垂直平分线l3也经过O点 评析：此题也是证明三条直线相交于一点的问题（即三线共点），通常先设两条直线相交于某一点，再证明这一点也在第三条直线上。 例2. 已知，如图，A、B是直线l同侧两点，试在l上找一个点P，使AP+BP的长度最短。 分析：点A、点B在直线l的同侧，直接找出P点的位置难度较大，我们可以换一个思路，设法将点A移到l的另一侧（A＇），欲使PA+PB最短，只要使A＇B最短即可，显然A＇、P、B三点应在一条直线上，从而确定出P点的位置。 解：（1）作出点A关于l的对称点A＇； （2）连结A＇B交l于点P，则点P是所求的点。 证明如下：连结PA ∵点A、点A＇关于直线l对称 ∴PA＝PA＇ ∵两点之间，线段最短 在l上再任取一点P＇，连结PA＇，P＇B ∴P＇A＇+P＇B>A＇B ∴PA＇+PB是连结A＇、B两点最短的线段 ∴PA+PB的长度最短 评析：由于两点之间线段最短，可以利用轴对称的方法将折线APB转化成线段A＇PB。 例3. 请你分别在下面三个网格（两相邻格点的距离均为1个单位长度）中，各设计一个图案，要求所设计的图案是轴对称图形，每个图形的面积等于4。 分析：由于三角形面积，长方形面积，梯形面积，因此可以同时考虑：（1）是轴对称图形；（2）面积为4。 解： 图中的等腰△ABC中，； 正方形ABCD中，S＝2×2＝4； 等腰梯形ABCD中， 评析：要尽可能使一边落在水平的格线上，那么它的高在竖直格线上，便于计算。 【模 ... ...