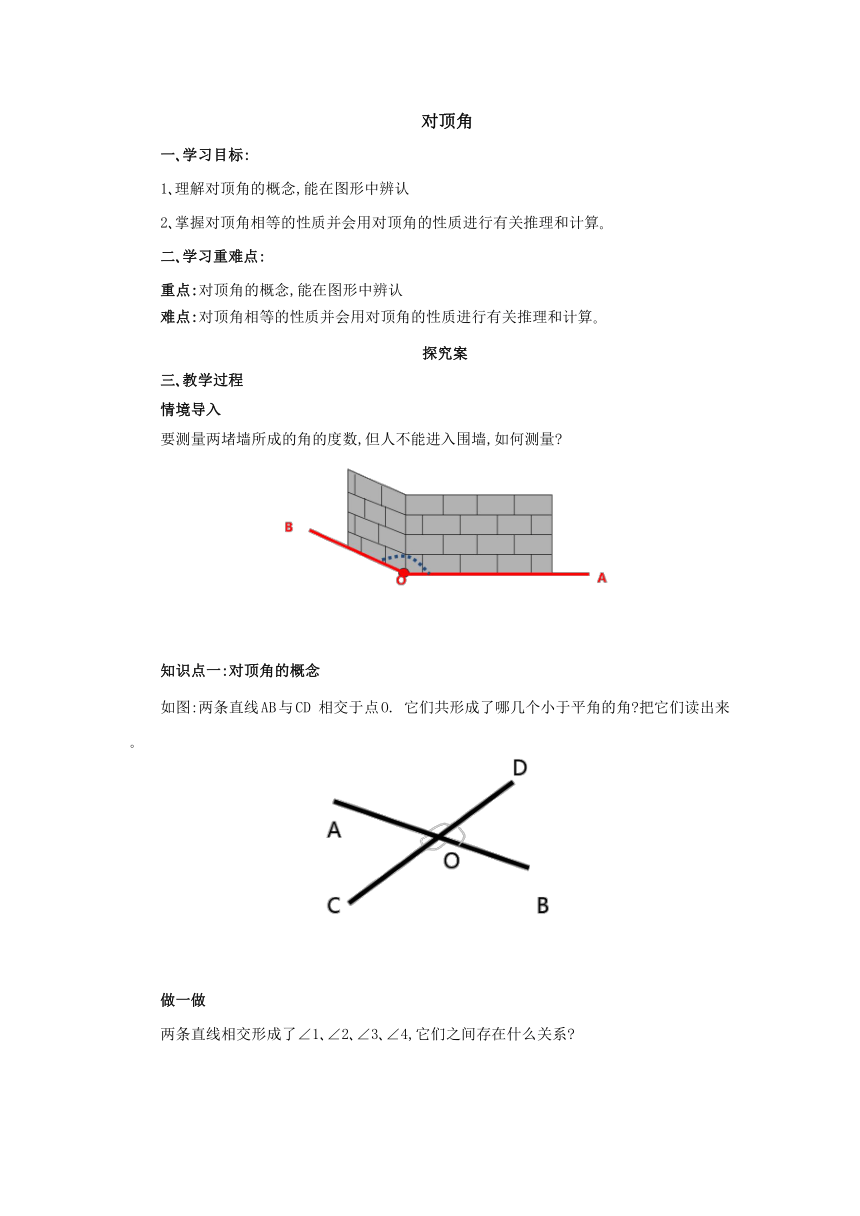
对顶角 一 学习目标: 1 理解对顶角的概念,能在图形中辨认 2 掌握对顶角相等的性质并会用对顶角的性质进行有关推理和计算 二 学习重难点: 重点:对顶角的概念,能在图形中辨认 难点:对顶角相等的性质并会用对顶角的性质进行有关推理和计算 探究案 三 教学过程 情境导入 要测量两堵墙所成的角的度数,但人不能进入围墙,如何测量 知识点一:对顶角的概念 如图:两条直线AB与CD 相交于点O. 它们共形成了哪几个小于平角的角 把它们读出来 做一做 两条直线相交形成了∠1 ∠2 ∠3 ∠4,它们之间存在什么关系 可以用度量法验证! 邻补角定义: 一条_____,且另一条边互为_____,这两个角称为互为邻补角. 如图可知, _____和_____ 互为邻补角, _____和_____也互为邻补角. 对顶角定义: 如果一个角的两边分别是另一个角两边的_____,那么这两个角是对顶角. 如图可知, _____和_____是对顶角, _____和_____也是对顶角. 例题解析 例1:下列各组角中,∠1与∠2是对顶角的是( ) 试一试 1.如图,直线a b相交于点O,若∠1等于40°,则∠2等于( ) A.50° B.60° C.140° D.160° 2.如图,直线AB CD EF相交于点O, (1)∠BOC的邻补角是_____ ; (2)∠AOD的对顶角是_____; (3)∠AOC的对顶角是_____. 3.下列各图中,∠l和∠2是对顶角吗 为什么 方法总结 对顶角的识别方法 判定两个角是否互为对顶角,要抓住对顶角的特征: (1)有公共顶点; (2)两个角的两边互为反向延长线; (3)在判断时要注意前提条件是两条直线相交,无公共边. 对顶角的特点: (1)顶点相同; (2)角的边互为反向延长线 知识点二:对顶角性质 想一想 如图,两条直线相交形成了∠1 ∠2 ∠3 ∠4,那么对顶角∠1与∠3相等吗 ∠2与∠4呢 归纳总结 性质:如果两个角是对顶角,那么这两个角_____ 简称: _____ 例题解析: 例2:如图所示,直线AB,CD交于点O,且∠BOC=80°,OE平分∠BOC,OF为OE的反向延长线. (1)求∠2和∠3的度数; (2)OF平分∠AOD吗 请说明理由. 试一试 1 如图,在△ABC中,BC=5,∠A=70°,∠B=75°,把△ABC沿直线BC的方向平移到△DEF的位置,若CF=3,则下列结论中错误的是( ) A. BE=3 B. ∠F=35° C. DF=5 D. AB∥DE 2 下列命题中,是真命题的为( ) A. 如果a>b,那么|a|>|b| B. 一个角的补角大于这个角 C. 平方后等于4的数是2 D. 直角三角形的两个锐角互余 问题解决 要测量两堵墙所成的角的度数,但人不能进入围墙,如何测量 随堂检测 1 如图,当光线从空气射入水中时,光线的传播方向发生了改变,这就是折射现象 .已知图中∠1=47°,∠2=30°, 则光的传播方向改变的度数为( ) A. 13° B. 15° C. 17° D. 19° 2 如图,直线AB,CD交于点O,OE平分∠AOD,OF平分∠BOD.已知∠AOF=160°,则∠COE=__ __. 3 如图,图中对顶角共有( )对. A.6 B.11 C.12 D.13 4 如图,直线AB EF相交于点D,∠ADC=900 (1)∠1的对顶角是_____;∠2的余角有_____ (2)若∠1与∠2的度数之比为1︰4, 求∠BDF的度数 5、如图,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE.若∠AOC=30°,则∠EOF=__ __. 6 如图,l1,l2,l3交于点O,∠1=∠2,∠3∶∠1=8∶1,求∠4的度数. 课堂小结 通过本节课的学习在小组内谈一谈你的收获,并记录下来: 我的收获 _____ 参考答案 探究案 知识点一:对顶角概念 ∠ AOD 、∠ BOD 、∠ BOC 、∠ AOC 做一做 邻补角定义: 一条边公共边,且另一条边互为反向延长线, 这两个角称为互为邻补角. 如图可知, ∠1和∠2 互为邻补角,∠3和∠4也互为邻补角. 对顶角定义: 如果一个角的两边分别是另一个角两边的反向延长线,那么这两个角是对顶角. 如图可知,∠1和∠3是对顶角, ∠2和∠4也是对顶角. 例题解析: 例1:D [解析] 根据两条直线相交,才能构成对顶角进行判断,A,B,C都不是由两条直线相交构成的图形,错误;D是由两条直线相交构成的图形,正确.故选D. 试一试 1.C ... ...
~~ 您好,已阅读到文档的结尾了 ~~

