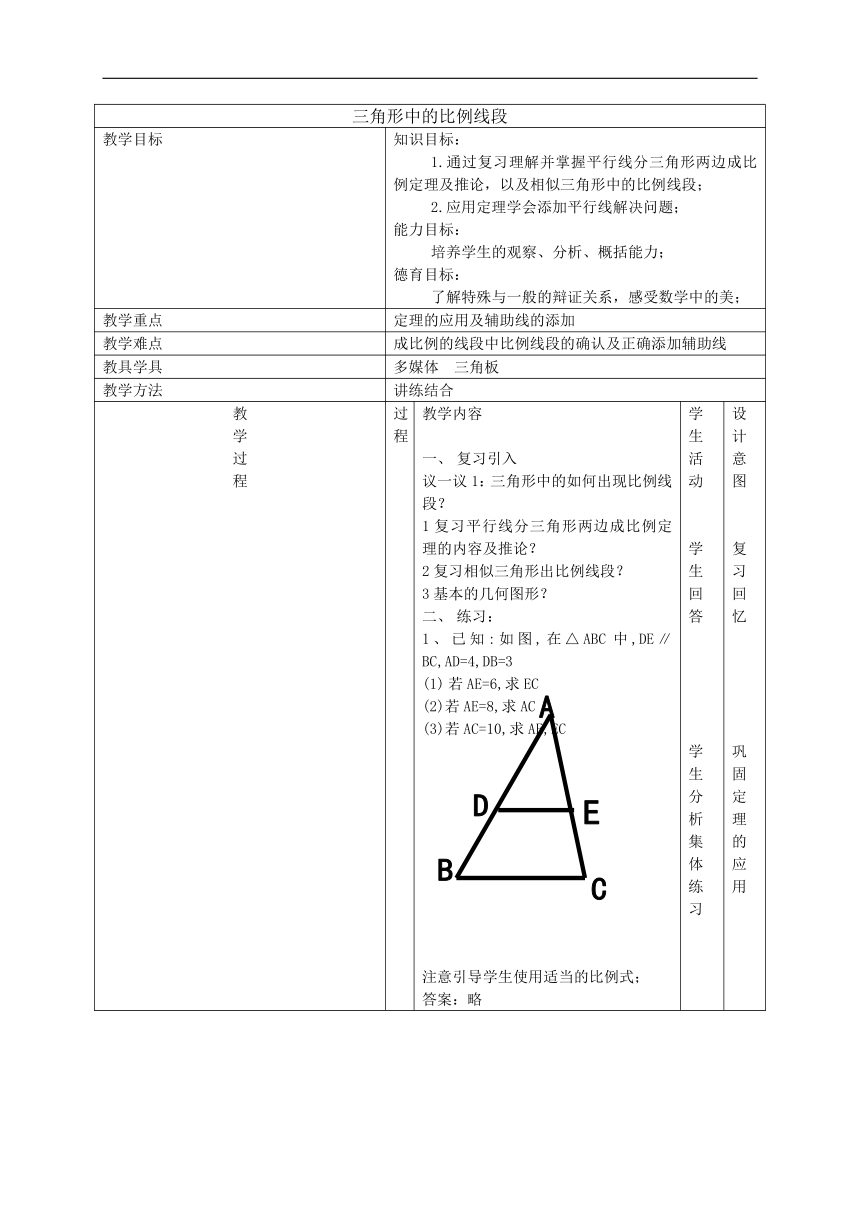
三角形中的比例线段 教学目标 知识目标: 1.通过复习理解并掌握平行线分三角形两边成比例定理及推论,以及相似三角形中的比例线段; 2.应用定理学会添加平行线解决问题; 能力目标: 培养学生的观察、分析、概括能力; 德育目标: 了解特殊与一般的辩证关系,感受数学中的美; 教学重点 定理的应用及辅助线的添加 教学难点 成比例的线段中比例线段的确认及正确添加辅助线 教具学具 多媒体 三角板 教学方法 讲练结合 教 学 过 程 教 学 过 程 过程 教学内容 复习引入 议一议1:三角形中的如何出现比例线段? 1复习平行线分三角形两边成比例定理的内容及推论? 2复习相似三角形出比例线段? 3基本的几何图形? 练习: 1、已知:如图,在△ABC中,DE∥BC,AD=4,DB=3 若AE=6,求EC (2)若AE=8,求AC (3)若AC=10,求AE,EC 注意引导学生使用适当的比例式; 答案:略 学生活动 学生回答 学生分析 集体练习 设计意图 复习回忆 巩固定理的应用 2、已知:如图,在△ABC中,DE∥BC,EF∥AB,试问: 成立吗?为什么? 引导学生分析,应用中间比解决问题,类比等量代换 3.已知:如图,在△ABC中, DE∥BC,EF∥AB. 试问: 成立吗 引导学生分析,多种方法解题, 1应用等线代换解决问题,类比等量代换 2应用相似三角形出比例线段解决问题 4、判断下列比例式是否正确 DE∥BC,EF∥AB1 (1) (2) (3) 练习 学生分析,解答 使学生掌握比例中中间比的应用 巩固定理应用,同时培养分析归纳能力 教 学 过 程 议一议2; 如图,AD是△ABC的中线,E是AC上任一点,BE交AD于点O,数学兴趣小组的同学在研究这个图形时,得到如下结论: (1)当时,; (2)当时,; (3)当时, 猜想,当时,(n是正整数),的一般结论,并说明理由。 分析: 1应用比例关系,需创造平行线,因此需要添加辅助线解决问题。 2辅助线添加方法: 过D点作DF∥BE交AC于点F(可以请学生用多种方法解题) 练习1 变式1: 小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°, BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求 的值 小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2). 请回答:的值为 . 变式2 参考小昊思考问题的方法,解决问题: 如图 3,在△ABC中,∠ACB=90°,点D在BC的延 长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 . (1)求 的值 (2)若CD=2,则BP= . 练习2 小明遇到一个问题:如图(1),在□ABCD中,点E是边BC的中点,点F是线段AE上 一点,BF的延长线交射线CD于点G. 如果求 的值 他的做法是:过点E作EH∥AB交BG于点H,则可以得 到△BAF∽△HEF. 请你回答(1)AB和EH的数量关系为 ,CG和EH的数量关系为 的值为 变式1 (2)如图(2),在原题的其他条件不变的情况下,如果 那么 的值为 (用含a的代数式表示) 变式2 (3)请你参考小明的方法继续探究:如图(3),在四边形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F. 如果 那么 的值为 (用含m,n的代数式表示). 学生进行练习 依照题意猜想 学生根据自身情况选择一小问进行证明 请学生都黑板上分析,用多种方法解题 阅读理解题意 结合问题所给思路解决问题 学生分析,解答 阅读理解题意 学生练习解答 结合第一问 进行变式练习 讨论分析 解决问题 巩固定理应用,同时培养分析归纳能力 加深对定理的理解 培养分析归纳能力 培养学生阅读理解题意分析解决问题的能力 培养学生阅读理解题意分析解决问题的能力 小结 课堂小结: 1.平行出比例2.平行出相似出比例 3.学会在复杂图形中寻找 A字图和8字图 板 书 设 计 三角形中的比例线段 1.平行出比例 例题 (图形) 2.平行出相似出比例 3.学会在复杂图形中寻找 A字图 ... ...
~~ 您好,已阅读到文档的结尾了 ~~