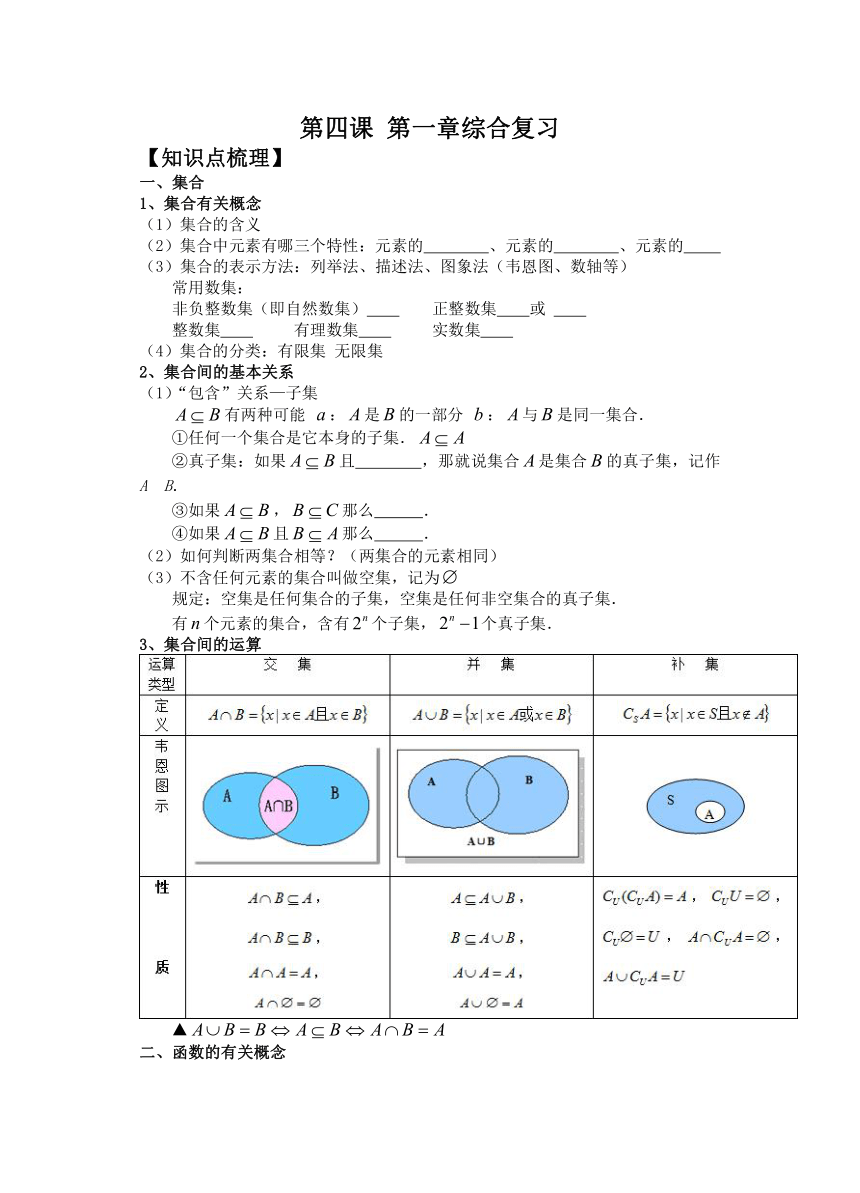
第四课 第一章综合复习 【知识点梳理】 一、集合 1、集合有关概念 (1)集合的含义 (2)集合中元素有哪三个特性:元素的 、元素的 、元素的 集合的表示方法:列举法、描述法、图象法(韦恩图、数轴等) 常用数集: 非负整数集(即自然数集) 正整数集 或 整数集 有理数集 实数集 (4)集合的分类:有限集 无限集 2、集合间的基本关系 (1)“包含”关系—子集 有两种可能 :是的一部分 :与是同一集合. ①任何一个集合是它本身的子集. ②真子集:如果且 ,那就说集合是集合的真子集,记作AB. ③如果,那么 . ④如果且那么 . (2)如何判断两集合相等?(两集合的元素相同) (3)不含任何元素的集合叫做空集,记为 规定:空集是任何集合的子集,空集是任何非空集合的真子集. 有个元素的集合,含有个子集,个真子集. 3、集合间的运算 ▲ 二、函数的有关概念 1、函数的概念 2、定义域:能使函数式有意义的实数的集合称为函数的定义域(或题意直接给出). 求函数的定义域有哪些常见类型? (1)分式的分母 ; (2)偶次方根的被开方数 ; (3)对数式的真数必须 ; (4)指数、对数式的底必须 且 ; (5)零次幂的指数不可以 ; (6)如果函数是由一些基本函数通过四则运算结合而成的,那么它的定义域是使各部分都有意义的的值组成的集合; (7)已知的定义域为,求的定义域,只需;已知的定义域,则的定义域为的值域; (8)实际问题中的函数的定义域还要保证实际问题有意义. 相同函数的判断方法:①表达式相同(与表示自变量和函数值的字母无关);②定义域一致 (两点必须同时具备) 3、函数的解析表达式 (1)函数的解析式是函数的一种表示方法,要求两个变量之间的函数关系时,一是要求出它们之间的对应法则,二是要求出函数的定义域. (2)求函数的解析式的方法 ①待定系数法②换元法③消元法(方程组法)④赋值法 三、函数的性质 1、函数的单调性 (1)增函数与减函数的定义(可用于判断函数的单调性) (2)图象的特点 如果函数在某个区间是增函数或减函数,那么说函数在这一区间上具有(严格的)单调性,在单调区间上增函数的图象从左到右是 的,减函数的图象从左到右是 的. (3)函数单调区间与单调性的判定方法 (A)定义法 ①任取,且; ②作差; ③变形(通常是因式分解和配方); ④定号(即判断差的正负); ⑤下结论(指出函数在给定的区间上的单调性). (B)观察图象法(从图象上看升降) (C)复合函数的单调性:“同增异减” (D)利用函数的运算性质(在公共定义域内) 增+增=增;减+减=减;增-减=增;减-增=减 注意:函数的单调区间只能是其定义域的子区间,不能把单调性相同的区间和在一起写成其并集. 2、函数的最值(值域) ①图象法②单调性法③反函数法④配方法⑤判别式法⑥换元法(⑦不等式法⑧数形结合法) 3、函数的奇偶性 (1)偶函数 一般地,对于函数的定义域内的任意一个,都有 ,那么就叫做偶函数. (2)奇函数 一般地,对于函数的定义域内的任意一个,都有 ,那么就叫做奇函数. (3)具有奇偶性的函数的图象的特征 偶函数的图象关于轴对称;奇函数的图象关于原点对称.特别地,如果奇函数的定义域包含有0,则 . 利用定义判断函数奇偶性的步骤: ①首先确定函数的定义域,并判断其是否关于原点对称; ②确定与的关系; ③作出相应结论:若或,则是偶函数;若或,则是奇函数. 【典型例题】 题型一 集合的基本关系与运算 例题1:已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},若B A,求实数m的取值范围. 例题2:已知方程x2+px+q=0的两个不相等实根分别为α,β,集合A={α,β},B={2,4,5,6},C={1,2,3,4},A∩C=A,A∩B=.求p,q的值. 变式1:已知集合A={x|2a+1≤ ... ...
~~ 您好,已阅读到文档的结尾了 ~~