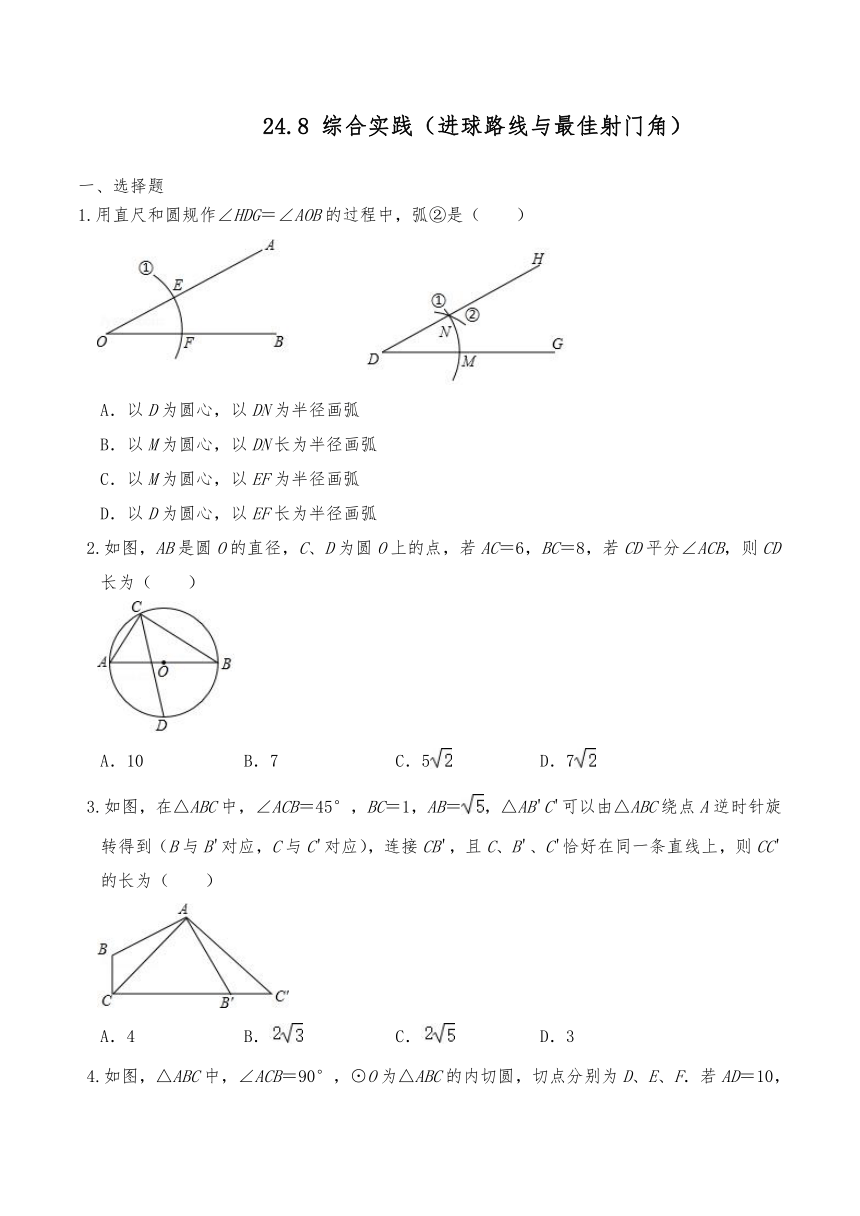
24.8 综合实践(进球路线与最佳射门角) 一、选择题 1.用直尺和圆规作∠HDG=∠AOB的过程中,弧②是( ) A.以D为圆心,以DN为半径画弧 B.以M为圆心,以DN长为半径画弧 C.以M为圆心,以EF为半径画弧 D.以D为圆心,以EF长为半径画弧 2.如图,AB是圆O的直径,C、D为圆O上的点,若AC=6,BC=8,若CD平分∠ACB,则CD长为( ) A.10 B.7 C.5 D.7 3.如图,在△ABC中,∠ACB=45°,BC=1,AB=,△AB'C'可以由△ABC绕点A逆时针旋转得到(B与B'对应,C与C'对应),连接CB',且C、B'、C'恰好在同一条直线上,则CC'的长为( ) A.4 B. C. D.3 4.如图,△ABC中,∠ACB=90°,⊙O为△ABC的内切圆,切点分别为D、E、F.若AD=10,BC=5,则OB的长为( ) A.4 B. C. D. 5.如图,AB是半径为6的⊙O上的一段弦,OC⊥AB于D,交⊙O于C,若CD=OB,则AB的长为( ) A.2 B.4 C.4 D.10 6.如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为4的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为( ) A.(﹣2,2) B.(﹣2,4) C.(﹣2,2) D.(2,2) 二、填空题 7.如图,P为等边三角形ABC内的一点,且P到三个顶点A,B,C的距离分别为3,4,5,则△ABC的面积为 . 8.如图,正六边形ABCDEF内接于⊙O,点P是直径AD上的一个动点,若⊙O的半径为2cm,则点P到这个正六边形六条边的距离之和为 cm. 9.如图,正八边形ABCDEFGH的两条对角线AC、BE相交于点P,∠EPC的度数为 . 10.如图,在Rt△ABC中,∠ACB=90°,∠BAC=33°,把△ABC绕点A按顺时针方向旋转33°,得到△A′B′C′,延长BC交B′C′于点D,则∠BDC′的度数是 . 11.已知线段AB是定值,平面内有一点C满足CB=AB,连AC,将线段AC绕点A逆时针旋转80°,得线段AD(如图示),连BD.当线段BD的长度最大时,则∠DCB= °. 12.如图,在Rt△ABC中,BF=BC,AB=4,现将△ABC绕点B顺时针旋转60°得到△BDE,此时点B、C、D恰好三点共线,则阴影面积为 ﹣ . 13.如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D是半径为4的⊙A上一动点,点M是CD的中点,则BM的最小值是 . 14.如图,正方形ABCD的边长为6,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C'D'的位置,B'C'与CD相交于点M,则点M的坐标为 . 三、解答题 15.如图所示,圆柱的高4cm,底面半径3cm,请求出该圆柱的表面积和体积. 16.如图,在△ABD中,AE、BE分别平分∠BAD和∠ABD.延长AE交△ABD的外接圆于点C,连接CB,CD,ED. (1)若∠CBD=40°,求∠BAD的度数. (2)求证:点C是△BDE的外心. 17.已知在⊙O中,直径AB⊥弦CD于G,E为DC延长线上一点 (1)如图1,BE交⊙O于点F,求证:∠EFC=∠BFD; (2)如图2,当CD也是直径,EF切⊙O于F,连接DF.若tan∠D=,求sin∠E的值. 18.如图,△ABC外切于⊙O,切点分别为D、E、F,BC=7,⊙O的半径为, (1)∠A=60°,求△ABC的周长. (2)若∠A=70°,点M为⊙O上异于F、E的动点,则∠FME的度数为 °. 19.如图,四边形ABCO为矩形,点A在x轴上,点C在y轴上,且点B的坐标为(﹣1,2),将此矩形绕点O顺时针旋转90°得矩形DEFO,抛物线y=﹣x2+bx+c过B,E两点. (1)求此抛物线的函数关系式; (2)将矩形ABCO向上平移,并且使此抛物线平分线段BC,求平移距离. 20.已知:如图,在Rt△ABC中,∠C=90°,Rt△ABC的内切圆⊙O,切点分别为点D、E、F, (1)若AC=3,BC=4,求△ABC的内切圆半径; (2)当AD=5,BD=7时,求△ABC的面 ... ...
~~ 您好,已阅读到文档的结尾了 ~~