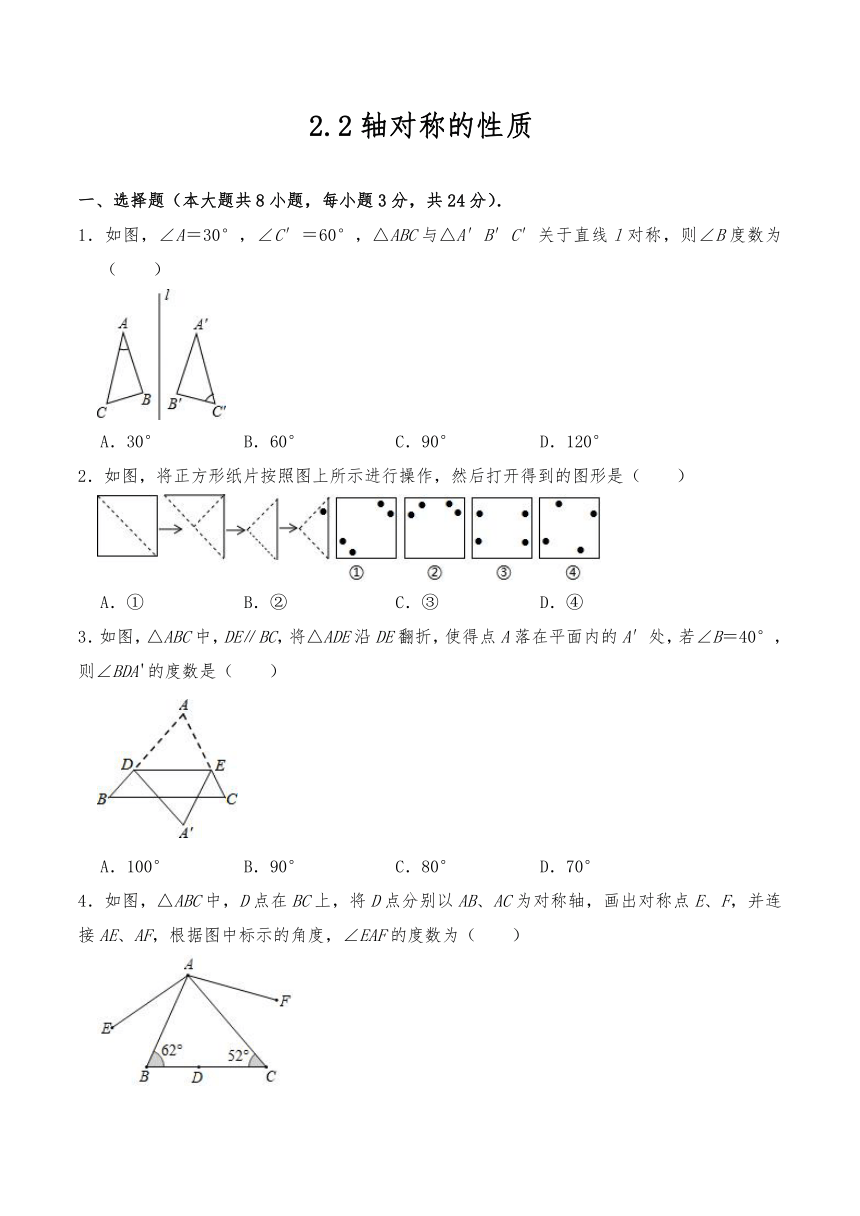
2.2轴对称的性质 一、选择题(本大题共8小题,每小题3分,共24分). 1.如图,∠A=30°,∠C′=60°,△ABC与△A′B′C′关于直线l对称,则∠B度数为( ) A.30° B.60° C.90° D.120° 2.如图,将正方形纸片按照图上所示进行操作,然后打开得到的图形是( ) A.① B.② C.③ D.④ 3.如图,△ABC中,DE∥BC,将△ADE沿DE翻折,使得点A落在平面内的A′处,若∠B=40°,则∠BDA'的度数是( ) A.100° B.90° C.80° D.70° 4.如图,△ABC中,D点在BC上,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF,根据图中标示的角度,∠EAF的度数为( ) A.126° B.128° C.130° D.132° 5.如图,△ABC中,C、C′关于AB对称,B、B′关于AC对称,D、E分别在AB、AC上,且C′D∥BC∥B′E,BE,CD交于点F,若∠BFD=α,∠A=β,则α与β之间的关系为( ) A.2β+α=180° B.α=2β C.α D.α=180° 6.如图,四边形ABCD中,AB=AD,点B关于AC的对称点B′恰好落在CD上,若∠BAD=110°,则∠ACB的度数为( ) A.40° B.35° C.60° D.70° 7.如图,△ABC与△DEF关于直线l对称,若∠A=65°,∠B=80°,则∠F=( ) A.80° B.65° C.45° D.35° 8.如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=106°,则∠C的度数( ) A.40° B.37° C.36 D.32° 二.填空题(共10小题) 9.如图,将△ABC沿直线折叠,折痕为EF.使点C落在AB边中点M上,若AB=8,AC=10,则△AEM的周长为 . 10.如图,在三角形纸片ABC中剪去∠C得到四边形ABDE,且∠C=40°,则∠1+∠2的度数为 . 11.如图,把Rt△ABC(∠C=90°)折叠,使A、B两点重合,得到折痕ED,若CE=DE,则∠A等于 . 12.如图,把一张长方形纸条ABCD沿EF折叠,若∠AEG=62°,则∠DEF= °. 13.如图,点P为∠AOB内任一点,E,F分别为点P关于OA,OB的对称点.若∠AOB=30°,则∠E+∠F= °. 14.如图,在四边形ABCD中,∠B=120°,∠B与∠ADC互为补角,点E在BC上,将△DCE沿DE翻折,得到△DC'E,若AB∥C'E,DC'平分∠ADE,则∠A的度数为 °. 15.如图的三角形纸片中,AB=6,AC=7,BC=5,沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,则△AED的周长为 . 16.如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在AB、AC上,将△ABC沿着DE折叠压平,A与A'重合,若∠1+∠2=140°,则∠A= . 17.如图,直线l是四边形ABCD的对称轴,AD∥BC,∠D=128°,则∠B的大小为 °. 18.如图,在四边形ABCD中,∠C+∠D=210°,E、F分别是AD,BC上的点,将四边形CDEF沿直线EF翻折,得到四边形C′D′EF,C′F交AD于点G,若△EFG有两个角相等,则∠EFG °. 三、解答题(本大题共4小题,共46分.) 19.如图,△ABC的三个顶点都在格点上. (1)直接写出点B的坐标; (2)画出△ABC关于x轴对称的△A1B1C1; (3)直接写出点A1的坐标. 20.如图,已知△ABC各顶点的坐标分别为A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1),直线l经过点(﹣1,0),并且与y轴平行,△A1B1C1与△ABC关于直线l对称. (1)画出△A1B1C1,并写出点A1的坐标 ; (2)若点P(m,n)是△ABC内一点,点P1是△A1B1C1内与点P对应的点,则点P1坐标 . 21.如图是8×8的正方形网格,每个小方格都是边长为1的正方形,在网格中建立平面直角坐标系xOy,使点A坐标为(2,﹣3),点B坐标为(4,﹣1). (1)试在图中画出这个直角坐标系; (2)标出点C(1,1),连接BC、AC,画出△ABC关于y轴对称的△A1B1C1. 22.如图, ... ...
~~ 您好,已阅读到文档的结尾了 ~~