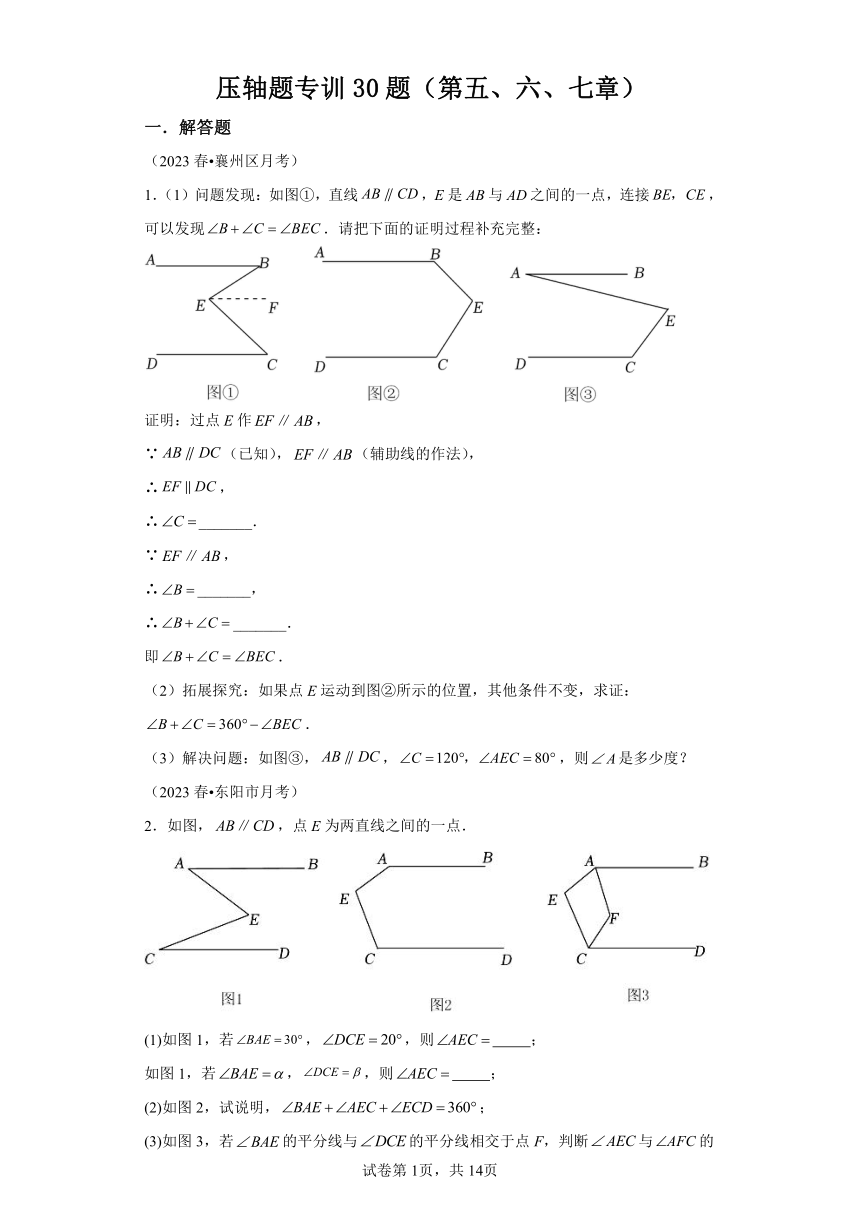
压轴题专训30题(第五、六、七章) 一.解答题 (2023春 襄州区月考) 1.(1)问题发现:如图①,直线,E是与之间的一点,连接,可以发现.请把下面的证明过程补充完整: 证明:过点E作, ∵(已知),(辅助线的作法), ∴, ∴_____. ∵, ∴_____, ∴_____. 即. (2)拓展探究:如果点E运动到图②所示的位置,其他条件不变,求证:. (3)解决问题:如图③,,,则是多少度? (2023春 东阳市月考) 2.如图,,点E为两直线之间的一点. (1)如图1,若,,则 ; 如图1,若,,则 ; (2)如图2,试说明,; (3)如图3,若的平分线与的平分线相交于点F,判断与的数量关系,并说明理由. (2023春 东台市月考) 3.把一块含角的直角三角尺放在两条平行线之间. (1)如图1,若三角形的角的顶点放在上,且,求的度数; (2)如图2,若把三角尺的两个锐角的顶点分别放在和上,请你探索并说明与间的数量关系; (3)如图3,若把三角尺的直角顶点放在上,角的顶点落在上,请直接写出与的数量关系. (2022秋 香坊区期末) 4.已知,平分交射线于点E,. (1)如图1,求证:; (2)如图2,点F是射线上一点,过点F作交射线于点G,点N是上一点,连接,来证:; (3)如图3,在(2)的条件下,连接,点P为延长线上一点,平分 交于点M,若平分,,,求的度数. (2022秋 翠屏区期末) 5.将一块三角板按如图①所示放置在锐角内,使直角边落在边上.现将三角板绕点B逆时针以每秒的速度旋转t秒(直角边旋转到如图②所示的位置),过点A作交射线于点M,平分,其中m的值满足:使代数式取得最小值. (1)求m的值; (2)当秒时,求的度数; (3)在某一时刻,当时,试求出与α之间的数量关系. (2023 广东模拟) 6.【学习新如】射到平面镜上的光线(入射光线)和反射后的光线(反射光线)与平面镜所夹的角相等.如图1,AB是平面镜,若入射光线与水平镜面夹角为,反射光线与水平镜面夹角为,则. (1)【初步应用】如图2,有两块平面镜,入射光线经过两次反射,得到反射光线,若,证明:; (2)【拓展探究】如图3,有三块平面镜,入射光线经过三次反射,得到反射光线,已知,若要使,则为多少度? (2022秋 朝阳区期末) 7.如图:,点E、F分别在直线、上,点P是、之间的一个动点. (1)如图①,当点P在线段左侧时,求证:、、之间的数量关系. (2)如图②,当点P在线段右侧时,、、之间的数量关系为 . (3)若、的平分线交于点Q,且,则 . (2022秋 道里区期末) 8.如图,直线与直线交于G,H,. (1)如图1,求证:; (2)如图2,点P在如图所示位置,连接,猜想之间的等量关系并给出证明; (3)如图3,在(2)的条件下,平分平分,求的度数. (2022秋 南岗区期末) 9.已知:直线EF分别交直线AB,CD于点G,H,且, (1)如图1,求证:; (2)如图2,点M,N分别在射线GE,HF上,点P,Q分别在射线CA,HC上,连接MP,NQ,且,分别延长MP,NQ交于点K,求证:; (3)如图3,在(2)的条件下,连接KH,KH平分,且HE平分,若,求的度数. (2022秋 射洪市期末) 10.【问题背景】 同学们,我们一起观察小猪的猪蹄,你会发现一个我们熟悉的几何图形,我们就把这个图形象的称为“猪蹄模型”,猪蹄模型中蕴含着角的数量关系. (1)如图①,,E为,之间一点,连接,,得到.试探究与、之间的数量关系,并说明理由. (2)【类比探究】请你利用上述“猪蹄模型”得到的结论或解题方法,完成下面的问题: 如图2,已知,,点E在上,,请你说明;(把下面的解答补充完整) 解:因为 所以 ( ) 因为( ) 又因为 所以 ( ) 即 所以 由(1)知 ∴ (3)【拓展延伸】如图3,平分,平分,.若,请直接写出的度数为 . (2022秋 三元区期末) 11.如图1,已知两条直线被直线所截, ... ...
~~ 您好,已阅读到文档的结尾了 ~~