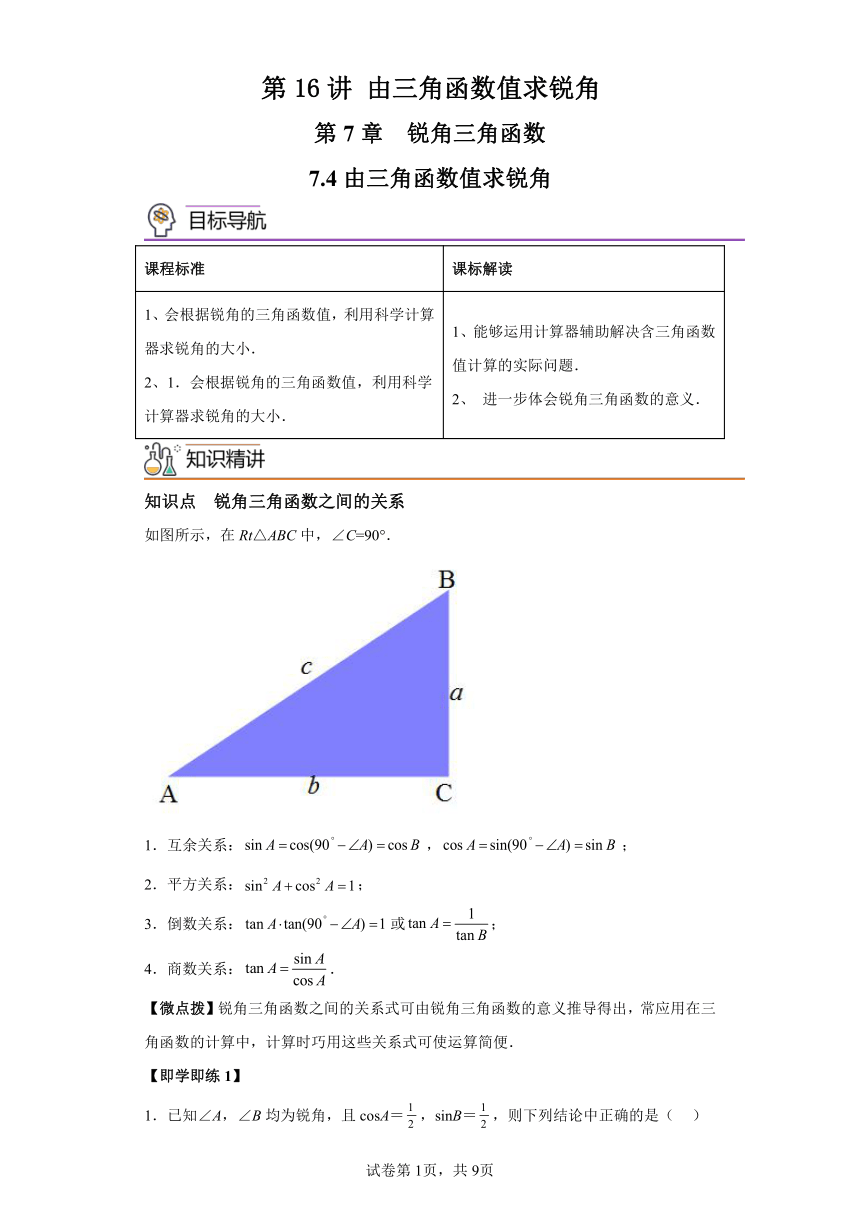
第16讲 由三角函数值求锐角 第7章 锐角三角函数 7.4由三角函数值求锐角 课程标准 课标解读 1、会根据锐角的三角函数值,利用科学计算器求锐角的大小. 2、1.会根据锐角的三角函数值,利用科学计算器求锐角的大小. 1、能够运用计算器辅助解决含三角函数值计算的实际问题. 2、 进一步体会锐角三角函数的意义. 知识点 锐角三角函数之间的关系 如图所示,在Rt△ABC中,∠C=90°. 1.互余关系:,; 2.平方关系:; 3.倒数关系:或; 4.商数关系:. 【微点拨】锐角三角函数之间的关系式可由锐角三角函数的意义推导得出,常应用在三角函数的计算中,计算时巧用这些关系式可使运算简便. 【即学即练1】 1.已知∠A,∠B均为锐角,且cosA=,sinB=,则下列结论中正确的是( ) A.∠A=∠B=60° B.∠A=∠B=30° C.∠A=30°,∠B=60° D.∠A=60°,∠B=30° 【即学即练2】 2.若,则ABC的形状是( ) A.含有60°直角三角形 B.等边三角形 C.含有60°的任意三角形 D.等腰直角三角形 考法01 根据特殊角三角函数值求角的度数 【典例1】 3.如图,将矩形绕点A旋转至矩形的位置,此时的中点恰好与点重合,交于点.若,则的面积为( ) A. B. C. D. 考法02 利用同角三角函数的关系求值 【典例2】 4.如图,平面直角坐标系中,四边形的边在轴正半轴上,轴,,点,连接,以为对称轴将翻折到,反比例函数的图象恰好经过点、,则的值是( ) A. B. C. D. 题组A 基础过关练 5.已知,则锐角α的度数是( ) A.60° B.45° C.30° D.75° 6.在△ABC中,∠C=90°,AB=,BC=1,则∠A的度数为( ) A. B. C. D. 7.若某斜面的坡度为,则该坡面的坡角的度数为( ) A. B. C. D. 8.在△ABC中,∠A和∠C都是锐角,且,,则△ABC的形状是( ) A.直角三角形 B.钝角三角形 C.等边三角形 D.不能确定 9.已知,则锐角的取值是( ) A. B. C. D. 10.在中,∠C=90°,CD⊥AB,垂足为点D,下列正确的是( ) A. B. C. D. 11.如果,那么锐角的度数为 °. 12.比较大小:sin50° sin60°(填“>”或“<”). 13.若为锐角,已知,那么 °. 14.如果是锐角,且,那么 度 题组B 能力提升练 15.下列说法正确的是( ) A.若|a|=a,则a>0 B.若,则锐角∠A=60° C.矩形的对角线互相垂直平分 D.菱形的面积等于对角线的乘积 16.△ABC中,∠A,∠B均为锐角,且(tanB-)(2sinA-)=0,则△ABC是( ) A.等腰三角形 B.等边三角形 C.直角三角形 D.至少一个角是60°的三角形 17.如图,在中,弦AB垂直平分半径OC,D为垂足,,则的长为( ) A. B. C. D. 18.如图,梯子,,两梯脚之间的距离BC的长为d.则d与l的关系式为( ) A. B. C. D. 19.如图,在矩形按以下步骤作图:①分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和;②作直线交于点;③连接,.若,,则的度数为( ) A. B. C. D. 20.如图,在矩形ABCD中,,,点E是CD边上一点,连接BE,将沿BE翻折,使点C恰好落在AD边上的点F处,则下列说法中错误的是( ) A. B. C. D. 21.在△ABC中,,则∠C= . 22.在中,,a,b,c分别是的对边.已知,那么 . 23.如图,已知直线l:y=x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,……;按此作法继续下去,则点M2020的坐标为 . 24.计算: (1)cos30°+sin45°; (2); (3)已知:中,,tanA=2,求的值. 题组C 培优拔尖练 25.如图,是的外接圆,为直径,交于点E,若点C为半圆的中点,弦,则的度数为( ) A. B. C. D. 26.如图,射线互相垂直,,点B位于射线的上 ... ...
~~ 您好,已阅读到文档的结尾了 ~~