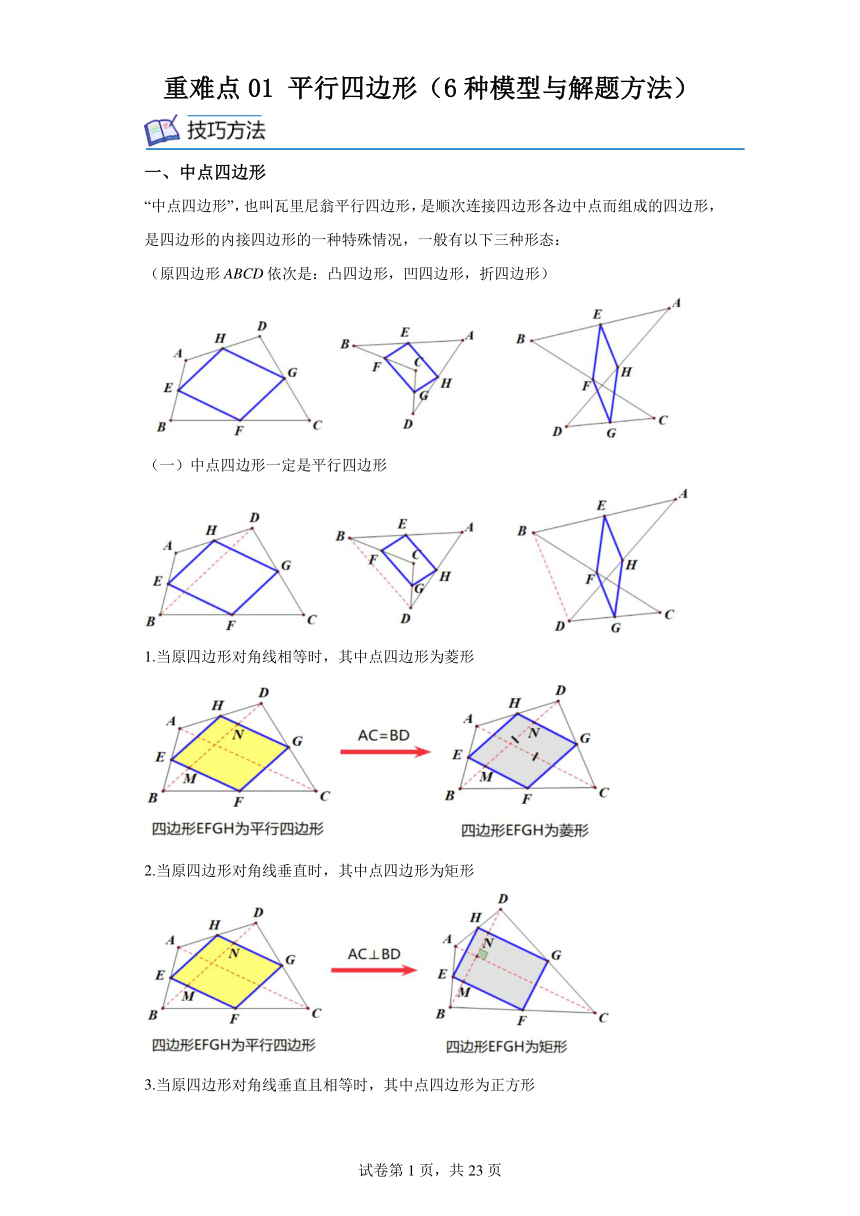
重难点01 平行四边形(6种模型与解题方法) 一、中点四边形 “中点四边形”,也叫瓦里尼翁平行四边形,是顺次连接四边形各边中点而组成的四边形,是四边形的内接四边形的一种特殊情况,一般有以下三种形态: (原四边形ABCD依次是:凸四边形,凹四边形,折四边形) (一)中点四边形一定是平行四边形 1.当原四边形对角线相等时,其中点四边形为菱形 2.当原四边形对角线垂直时,其中点四边形为矩形 3.当原四边形对角线垂直且相等时,其中点四边形为正方形 (二)中点四边形的周长等于原四边形对角线之和 (三)中点四边形的面积等于原四边形面积的二分之一 二、十字架模型 模型展示: 1.若正方形的四条边上存在互相垂直的十字架;则十字架长度相等; 2.在正方形的两组对边分别各取两点并相连,所得两条线段如果垂直,那么相等; 3.若矩形的四条边上存在互相垂直的十字架;则十字架长度之比等于矩形邻边之比. 三、梯子模型 梯子问题果非常重要的一类最值问题,关键点在于取梯子的中点运用斜边中线和勾股定理来解决,得到两条线段的和是所求的最大值. 例题:如图所示,一根长2.5米的木棍AB斜靠在与地面垂直的墙上,此时墙角O与木棍B端的距离为1.5米,设木棍的中点为P,若木棍A端沿墙下滑,则B端沿地面向右滑行. (1)木棍在滑动过程中,线段OP的长度发生改变了吗 请说明理由;若不变,求OP的长. 梯子下滑的过程中P离墙角的距离都是一样的. (2)如果木棍的底端B向外滑出0.9米,那么木棍的顶端A沿墙下滑多少米 梯子下滑的过程中P离墙角的距离都是一样的. 取公共边中点是关键,辅助线添加构造模型 直角三角形斜边上的中线等于斜边的一半 四、对角互补模型 模型1:全等形一-90°对角互补模型 模型2:全等形--120°对角互补模型 模型 3:全等形一一任意角对角互补模型 模型4:相似形一-90°对角互补模型(后面会学到) 五、与正方形有关三垂线 六、正方形与45°角的基本图 题型一:中点四边形 一、单选题 (2022春·贵州遵义·八年级校考期中) 1.我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形,下列说法正确的是 A.任意一个四边形的中点四边形是菱形 B.任意一个平行四边形的中点四边形是平行四边形 C.对角线相等的四边形的中点四边形是矩形 D.对角线垂直的四边形的中点四边形是正方形 二、填空题 (2021春·广西来宾·八年级统考期中) 2.依序连接菱形各边中点所得的四边形是 (指特殊四边形). (2021春·新疆省直辖县级单位·八年级统考期末) 3.顺次连结对角线相等且垂直的四边形各边中点所得的四边形是 . (2022春·上海闵行·八年级上海市民办文绮中学校考阶段练习) 4.若顺次连接四边形ABCD四边中点所得的四边形是菱形,则原四边形的对角线AC、BD所满足的条件是 . (2020春·江苏常州·八年级统考期末) 5.若顺次连接四边形ABCD四边中点形成的四边形为矩形,则四边形ABCD满足的条件为. 三、解答题 (2021春·江苏泰州·八年级高港实验学校校考阶段练习) 6.如图1,在四边形中,如果对角线和相交并且相等,那么我们把这样的四边形称为等角线四边形. (1)①在“平行四边形、矩形、菱形”中,_____一定是等角线四边形(填写图形名称); ②若、、、分别是等角线四边形四边、、、的中点,当对角线、还要满足_____时,四边形是正方形. (2)如图2,已知在中,,,,为平面内一点. ①若四边形是等角线四边形,且,求符合条件的等角线四边形的面积. ②设点是所在平面上的任意一点且,若四边形是等角线四边形,求出四边形面积的最大值,并说明理由. (2021春·广西桂林·八年级统考期末) 7.如图,四边形ABCD的四边中点分别为E、F、G、H,顺次连接E、F、G、H. (1)判断四边形EFGH形 ... ...
~~ 您好,已阅读到文档的结尾了 ~~