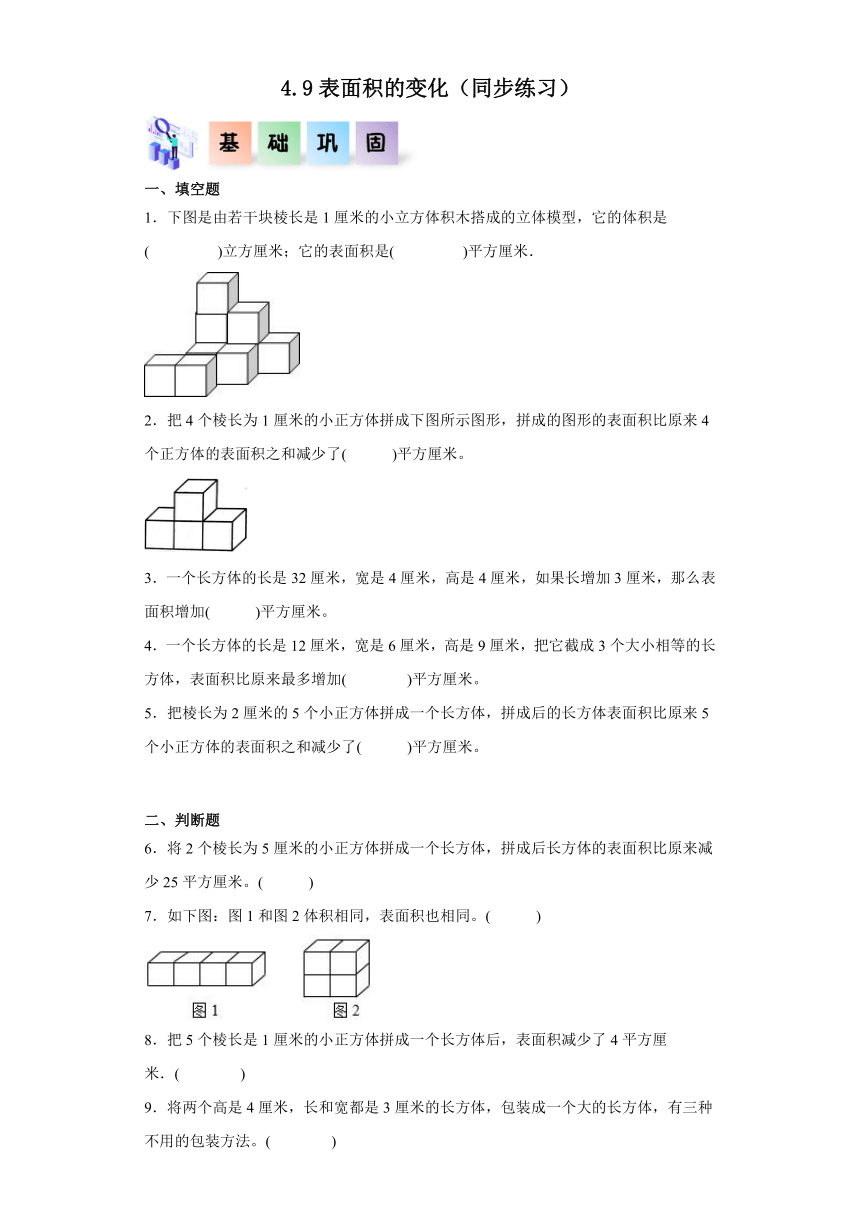
4.9表面积的变化(同步练习) 一、填空题 1.下图是由若干块棱长是1厘米的小立方体积木搭成的立体模型,它的体积是( )立方厘米;它的表面积是( )平方厘米. 2.把4个棱长为1厘米的小正方体拼成下图所示图形,拼成的图形的表面积比原来4个正方体的表面积之和减少了( )平方厘米。 3.一个长方体的长是32厘米,宽是4厘米,高是4厘米,如果长增加3厘米,那么表面积增加( )平方厘米。 4.一个长方体的长是12厘米,宽是6厘米,高是9厘米,把它截成3个大小相等的长方体,表面积比原来最多增加( )平方厘米。 5.把棱长为2厘米的5个小正方体拼成一个长方体,拼成后的长方体表面积比原来5个小正方体的表面积之和减少了( )平方厘米。 二、判断题 6.将2个棱长为5厘米的小正方体拼成一个长方体,拼成后长方体的表面积比原来减少25平方厘米。( ) 7.如下图:图1和图2体积相同,表面积也相同。( ) 8.把5个棱长是1厘米的小正方体拼成一个长方体后,表面积减少了4平方厘米.( ) 9.将两个高是4厘米,长和宽都是3厘米的长方体,包装成一个大的长方体,有三种不用的包装方法。( ) 10.把8个小正方体拼成一个大的正方体,然后拿走一个小正方体(如图),这时图形的表面积和拼成的大正方体的表面积相同.( ) 三、选择题 11.下边图中,比较它们的表面积,我认为( )。 A.甲表面积大 B.乙表面积大 C.表面积一样大 D.无法比较 12.四个一样的立方体纸箱放在墙角,与如图露在外面的面的数量相等的摆法是( )。 A.B.C.D. 13.下列立体图形是由16块1cm 的小正方体木块拼摆而成的,图( )的表面积最小。 A. B. C. D. 14.把1米长的长方体木料锯成三段,表面积比原来增加了0.6平方分米,原来这根木料的体积是( )。 A.20立方分米 B.1.5立方分米 C.60立方分米 15.把两个棱长都是2分米的正方体拼成一个长方体,这个长方体的表面积比两个正方体的表面积的和减少了( )平方分米。 A.4 B.8 C.16 四、解答题 16.把一个长、宽、高分别是9厘米、6厘米、5厘米的长方体截成两个小长方体,表面积最多增加多少平方厘米?最少增加多少平方厘米? 17.一位玩具制作者从一块长、宽、高分别是30cm、14cm、10cm的长方体木块中切取棱长3cm的小正方体(要求取得尽可能多).结果剩下的木块如下图所示(L形).被切掉的小正方体有多少块?剩下的L形木块的表面积是多少? 1. 10 38 2.6 【分析】根据图形可知,拼成的图形表面积比原来4个正方体的表面积之和减少了6个正方形面积,利用正方形面积公式:边长×边长即可解答。 【详解】1×1×6=6(平方厘米) 【分析】此题主要考查关于表面积减少的实际应用解题,需要理解拼成的图形表面积比原来4个正方体的表面积之和减少了6个正方形面积。 3.48 【分析】根据题意可知,如果长增加3厘米,那么增加的是4个长方形面积,即(长×高+长×宽)×2,以此解答。 【详解】(3×4+3×4)×2 =(12+12)×2 =24×2 =48(平方厘米) 【分析】此题主要考查关于表面积增加的实际应用解题,需要理解如果长增加3厘米,那么增加的是4个长方形面积,即(长×高+长×宽)×2,也可以画图进行理解。 4.432 【分析】一个长方体被截成3个大小相等的长方体,可知表面积增加了4个相同的横截面,要使表面积增加的最多,则增加横截面的长、宽分别是12厘米、9厘米,据此解答。 【详解】12×9×4=432(平方厘米) 【分析】解答此题的关键是找出增加的表面积部分指的是哪几个面,注意题目要求表面积增加最多,找相对较大的两个数做横截面的长、宽。 5.32 【分析】根据题意可知,5个小正方体拼成一个长方体,拼成后的长方体表面积比原来5个小正方体的表面积之和减少了8个正方形面积,利用正方形面积公式:边长×边长即可 ... ...
~~ 您好,已阅读到文档的结尾了 ~~