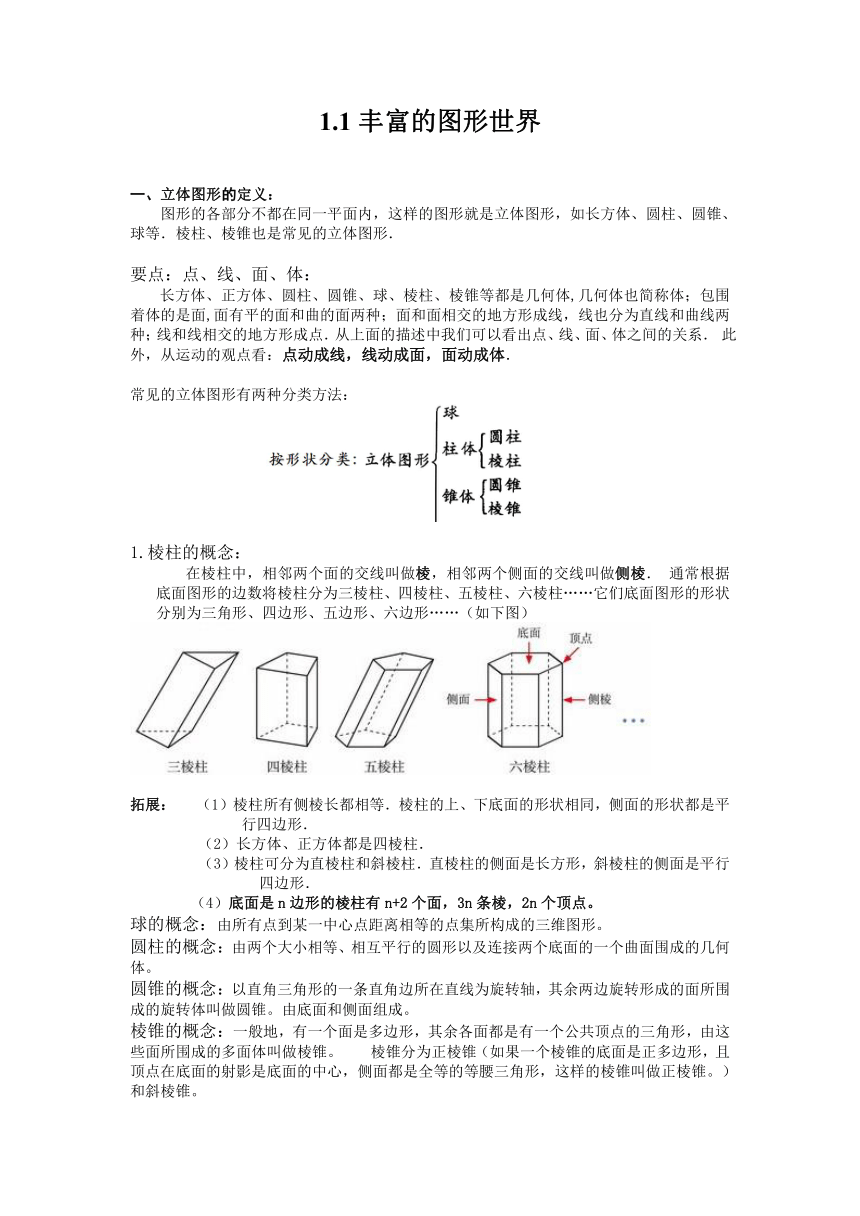
1.1丰富的图形世界 一、立体图形的定义: 图形的各部分不都在同一平面内,这样的图形就是立体图形,如长方体、圆柱、圆锥、球等.棱柱、棱锥也是常见的立体图形. 要点:点、线、面、体: 长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体,几何体也简称体;包围着体的是面,面有平的面和曲的面两种;面和面相交的地方形成线,线也分为直线和曲线两种;线和线相交的地方形成点.从上面的描述中我们可以看出点、线、面、体之间的关系. 此外,从运动的观点看:点动成线,线动成面,面动成体. 常见的立体图形有两种分类方法: 1.棱柱的概念: 在棱柱中,相邻两个面的交线叫做棱,相邻两个侧面的交线叫做侧棱. 通常根据底面图形的边数将棱柱分为三棱柱、四棱柱、五棱柱、六棱柱……它们底面图形的形状分别为三角形、四边形、五边形、六边形……(如下图) 拓展: (1)棱柱所有侧棱长都相等.棱柱的上、下底面的形状相同,侧面的形状都是平行四边形. (2)长方体、正方体都是四棱柱. (3)棱柱可分为直棱柱和斜棱柱.直棱柱的侧面是长方形,斜棱柱的侧面是平行四边形. (4)底面是n边形的棱柱有n+2个面,3n条棱,2n个顶点。 球的概念:由所有点到某一中心点距离相等的点集所构成的三维图形。 圆柱的概念:由两个大小相等、相互平行的圆形以及连接两个底面的一个曲面围成的几何体。 圆锥的概念:以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥。由底面和侧面组成。 棱锥的概念:一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥。 棱锥分为正棱锥(如果一个棱锥的底面是正多边形,且顶点在底面的射影是底面的中心,侧面都是全等的等腰三角形,这样的棱锥叫做正棱锥。)和斜棱锥。 二、展开与折叠 有些立体图形是由一些平面图形围成,将它们的表面适当剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的展开图. 一.正方体的11种展开图 1.“一四一”型 一、三层的两个面是相对面,第二层四个面中不相邻的两个面是相对面. 2.“二三一”型 中间层中不相邻的两个面一定是相对面,中间的那个面与离它最远的面是相对面;余下的两个面是相对面. 3.“二二二”型 相邻两层不相邻的两个面一定是相对面,这样就可以先确定出两对不同的相对面,剩下的两个面一定是相对面. 4.“三三”型 每层中不相邻的两个面是相对面,剩下的两个面是相对面. 二.圆柱、棱柱的展开图 圆柱 直棱柱 三.圆锥、棱锥的展开图 圆锥 棱锥 三、截一个几何体 用一个平面去截一个几何体,截出的面叫做截面.截面的形状可能是三角形、四边形、五边形、六边形或圆等等. 如下图所示,分别用四个不同的平面去截一个正方体,所得到的图形。 四、从三个方向看物体的形状 一般是从以下三个方向:(如下图) (1)从正面看;在正面内得到的由前向后观察物体的视图,叫做主视图。 (2)从左面看;在水平面内得到的由上向下观察物体的视图,叫做俯视图。 (3)从上面看;在侧面内得到的由左向右观察物体的视图,叫做左视图。 要点:1 .主视图与俯视图表示同一物体的长,主视图与左视图表示同一物体的高,左视图与俯视图表示同一物体的宽;主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等。 2.看得见部分的轮廓线画成实线。 3.看不见部分的轮廓线画成虚线。 考点1:认识立体图形 例1.(2023 西城区一模)下面几何体中,是圆柱的是( ) B. C. D. 考点二: 点、线、面、体 例2.(2022秋 湖北期末)将最左边的图形绕直线l旋转一周后得到的图形是( ) A. B. C. D. 考点三:几何体的展开图 例3.(2023 衡水三模)将如图所示的 ... ...
~~ 您好,已阅读到文档的结尾了 ~~