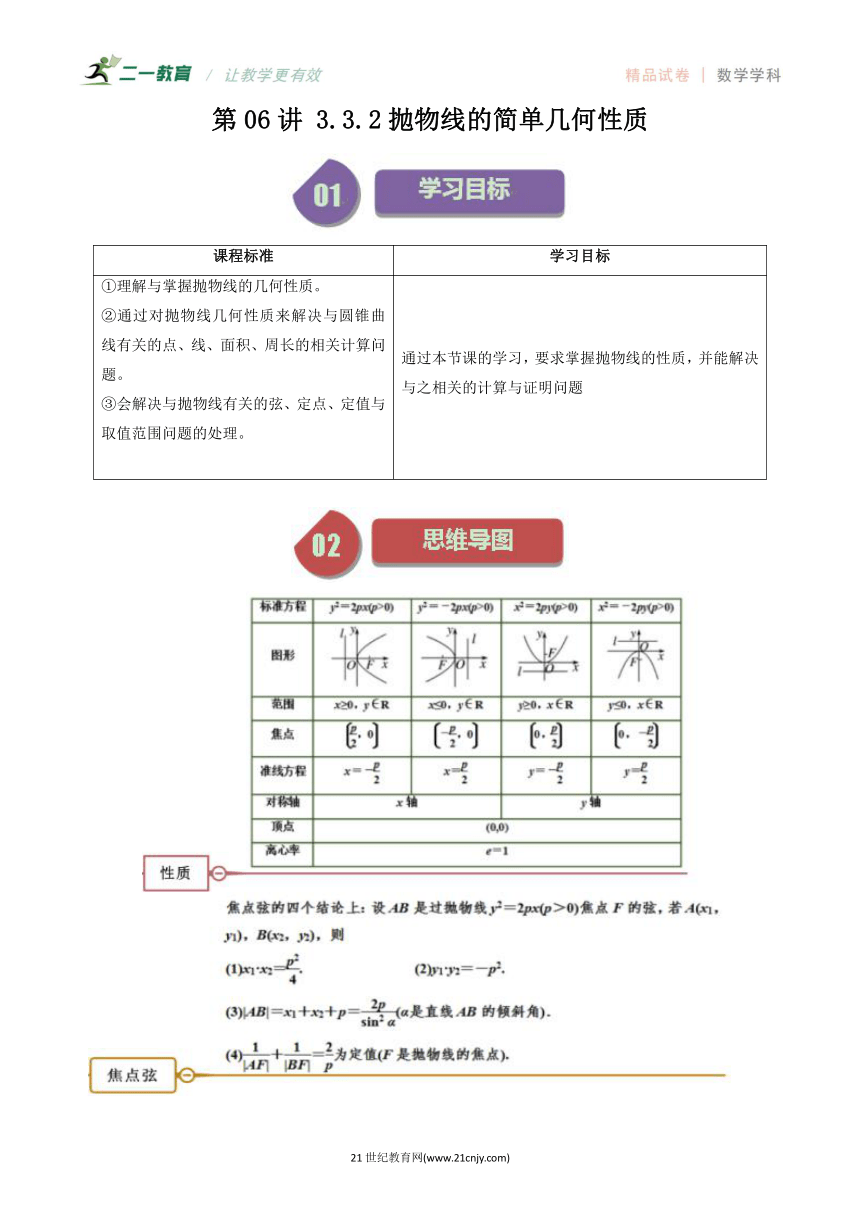
第06讲 3.3.2抛物线的简单几何性质 课程标准 学习目标 ①理解与掌握抛物线的几何性质。 ②通过对抛物线几何性质来解决与圆锥曲线有关的点、线、面积、周长的相关计算问题。 ③会解决与抛物线有关的弦、定点、定值与取值范围问题的处理。 通过本节课的学习,要求掌握抛物线的性质,并能解决与之相关的计算与证明问题 知识点01:抛物线的简单几何性质 标准方程 () () () () 图形 范围 , , , , 对称轴 轴 轴 轴 轴 焦点坐标 准线方程 顶点坐标 离心率 通径长 知识点02:直线与抛物线的位置关系 设直线:,抛物线:(),将直线方程与抛物线方程联立整理成关于的方程 (1)若,当时,直线与抛物线相交,有两个交点; 当时,直线与抛物线相切,有一个切点; 当时,直线与抛物线相离,没有公共点. (2)若,直线与抛物线有一个交点,此时直线平行于抛物线的对称轴或与对称轴重合.因此直线与抛物线有一个公共点是直线与抛物线相切的必要不充分条件. 【即学即练1】(2023·全国·高三专题练习)直线与抛物线的位置关系为( ) A.相交 B.相切 C.相离 D.不能确定 【答案】A 【详解】直线过定点, ∵, ∴在抛物线内部, ∴直线与抛物线相交, 故选:A. 知识点03:直线和抛物线 1、抛物线的通径(过焦点且垂直于轴的弦)长为. 2、抛物线的焦点弦 过抛物线()的焦点的一条直线与它交于两点,,则 ①,;②;③. 【即学即练2】(2023秋·四川成都·高二校考期末)已知抛物线,其焦点到其准线的距离为,过焦点且倾斜角为的直线交抛物线于两点, (1)求抛物线的方程及其焦点坐标; (2)求. 【答案】(1),焦点坐标为;(2)8. 【详解】解:(1)抛物线的焦点到其准线的距离为,得, 所以抛物线的方程为,焦点坐标为. (2)过焦点且倾斜角为的直线的方程为,设, 联立方程组消去可得,则, 所以. 说明:抛物线的焦半径公式如下:(为焦准距) (1)焦点在轴正半轴,抛物线上任意一点,则; (2)焦点在轴负半轴,抛物线上任意一点,则; (3)焦点在轴正半轴,抛物线上任意一点,则; (4)焦点在轴负半轴,抛物线上任意一点,则. 题型01抛物线的简单性质 【典例1】(2023春·四川广安·高二四川省广安友谊中学校考阶段练习)抛物线C与抛物线关于轴对称,则抛物线C的准线方程是( ) A. B. C. D. 【典例2】(2023·全国·高三专题练习)对抛物线,下列描述正确的是( ) A.开口向上,焦点为 B.开口向上,焦点为 C.开口向右,焦点为 D.开口向右,焦点为 【典例3】(2023秋·高二课时练习)根据下列条件写出抛物线的标准方程: (1)焦点是; (2)准线方程是; (3)焦点到准线的距离是. 【变式1】(2023秋·陕西西安·高二校考期末)对抛物线,下列描述正确的是 A.开口向上,焦点为 B.开口向上,焦点为 C.开口向右,焦点为 D.开口向右,焦点为 【变式2】(2023春·湖南长沙·高二长沙市明德中学校考期中)若抛物线的焦点与双曲线的右焦点重合,则的值 . 题型02直线与抛物线的位置关系 【典例1】(2023秋·高二课时练习)已知直线,抛物线,l与有一个公共点的直线有( ) A.1条 B.2条 C.3条 D.1条、2条或3条 【典例2】(多选)(2023·全国·高三专题练习)若经过点的直线与抛物线恒有公共点,则C的准线可能是( ). A. B. C. D. 【典例3】(2023春·湖北孝感·高二校联考阶段练习)已知M是抛物线上一点,则点M到直线的最短距离为 . 【典例4】(2023秋·广西北海·高二统考期末)已知抛物线,其准线方程为. (1)求抛物线的方程; (2)不过原点的直线与抛物线交于不同的两点,且,求的值. 【变式1】(2023·全国·高三专题练习)已知抛物线与直线有且仅有一个交点,则( ) A.4 B.2 C.0或4 D.8 【变式2】(多选) ... ...
~~ 您好,已阅读到文档的结尾了 ~~