专题强化4　动力学中的连接体问题 学案

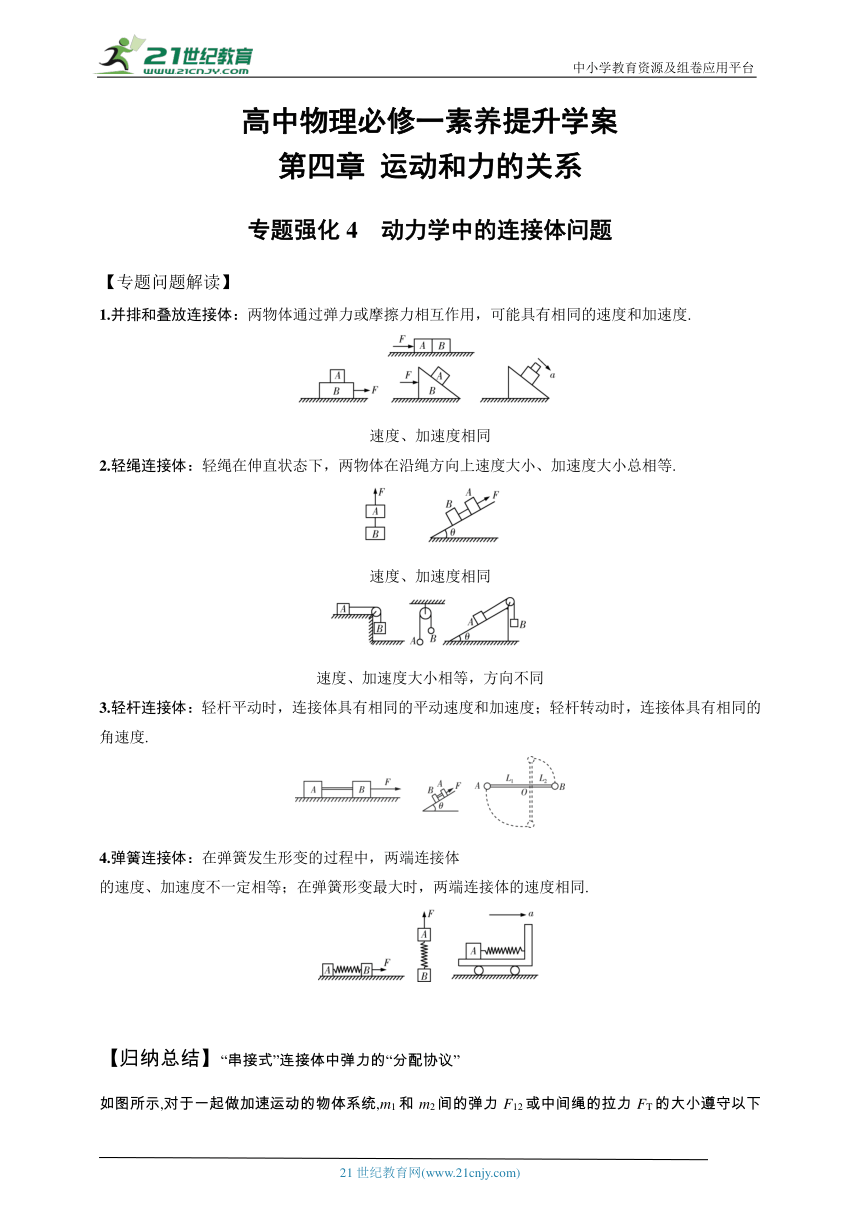
中小学教育资源及组卷应用平台 高中物理必修一素养提升学案 第四章 运动和力的关系 专题强化4　动力学中的连接体问题 【专题问题解读】 1.并排和叠放连接体：两物体通过弹力或摩擦力相互作用，可能具有相同的速度和加速度. 速度、加速度相同 2.轻绳连接体：轻绳在伸直状态下，两物体在沿绳方向上速度大小、加速度大小总相等. 速度、加速度相同 速度、加速度大小相等，方向不同 3.轻杆连接体：轻杆平动时，连接体具有相同的平动速度和加速度；轻杆转动时，连接体具有相同的角速度. 4.弹簧连接体：在弹簧发生形变的过程中，两端连接体 的速度、加速度不一定相等；在弹簧形变最大时，两端连接体的速度相同. 【归纳总结】“串接式”连接体中弹力的“分配协议” 如图所示,对于一起做加速运动的物体系统,m1和m2间的弹力F12或中间绳的拉力FT的大小遵守以下力的“分配协议”: (1)若外力F作用于m1上,则F12=FT=; (2)若外力F作用于m2上,则F12=FT=。 注意:①此“协议”与有无摩擦无关(若有摩擦,两物体与接触面间的动摩擦因数必须相同); ②此“协议”与两物体间有无连接物、何种连接物(轻绳、轻杆、轻弹簧)无关; ③物体系统处于水平面、斜面或竖直方向上一起加速运动时此“协议”都成立。 【分类解析】 一、加速度和速度都相同的连接体问题 【典例1】　如图所示,光滑水平面上A、B两物体用不可伸长的水平轻绳相连,用水平力F拉A使A、B一起运动,A的质量为mA、B的质量为mB,求: (1)A、B一起运动的加速度大小; (2)A、B两物体间绳的拉力FT的大小。 答案　(1)　(2)F 解析　(1)把A、B作为一个整体,有 F=(mA+mB)a 解得a= (2)单独分析B,FT=mBa 得FT=F。 拓展1　在例1中,若两物体与水平面间的动摩擦因数均为μ,则A、B间绳的拉力为多大 答案　F 解析　若动摩擦因数均为μ,以A、B整体为研究对象,有F-μ(mA+mB)g=(mA+mB)a,然后隔离B为研究对象,有FT-μmBg=mBa,联立解得FT=F。 拓展2　如图所示,物体A、B用不可伸长的轻绳连接,在竖直向上的恒力F作用下一起向上做匀加速直线运动,已知mA=10 kg,mB=20 kg,F=600 N,不计空气阻力,求此时轻绳对物体B的拉力大小。(g取10 m/s2) 答案　400 N 解析　对A、B整体受力分析,再单独对B受力分析,分别如图甲、乙所示: 对A、B整体,根据牛顿第二定律有: F-(mA+mB)g=(mA+mB)a 物体B受轻绳的拉力和重力,根据牛顿第二定律有: FT-mBg=mBa, 联立解得FT=400 N。 拓展3　如图所示,若把两物体放在固定斜面上,两物体与斜面间的动摩擦因数均为μ,在方向平行于斜面向上的拉力F作用下沿斜面向上加速,A、B间绳的拉力为多大 答案　F 解析　以A、B整体为研究对象, 设斜面的倾角为θ,F-(mA+mB)gsin θ-μ(mA+mB)gcos θ=(mA+mB)a, 以B为研究对象, FT-mBgsin θ-μmBgcos θ=mBa, 联立解得 F=F。 二、加速度和速度大小相等、方向不同的连接体问题 【典例2】(多选)如图所示,在光滑的水平桌面上有一个质量为3m的物体A,通过绳子与质量为m的物体B相连,假设绳子、定滑轮的质量以及绳子与定滑轮之间的摩擦力都忽略不计,绳子不可伸长。重力加速度为g,将两物体同时由静止释放,则下列说法正确的是 (　　) A.物体A的加速度大小为g B.物体B的加速度大小为g C.绳子的拉力大小为mg D.物体B处于失重状态 答案　AD 解析　静止释放后,物体A将向右做加速运动,物体B将加速下落,二者加速度大小相等,由牛顿第二定律, 对A:FT=3ma 对B:mg-FT=ma 解得a=g,FT=mg。物体B加速度方向竖直向下,处于失重状态,故选A、D。 拓展1　若将B换成一个竖直向下且大小为mg的力,则物体A的加速度为多大 答案　对A:FT=3ma FT=mg 解得a=g。 拓展2　如图所示,在例2中,若平面MN变为倾角为37°的光滑斜面,求两物体的加速度大小及绳子的拉力大小。(已知sin 37°=0.6) 答案　0.2g　1.2mg 解析　对A: ... ...