2025年中考数学二轮专题复习-专题一　全等模型高效拆分特训（含答案）

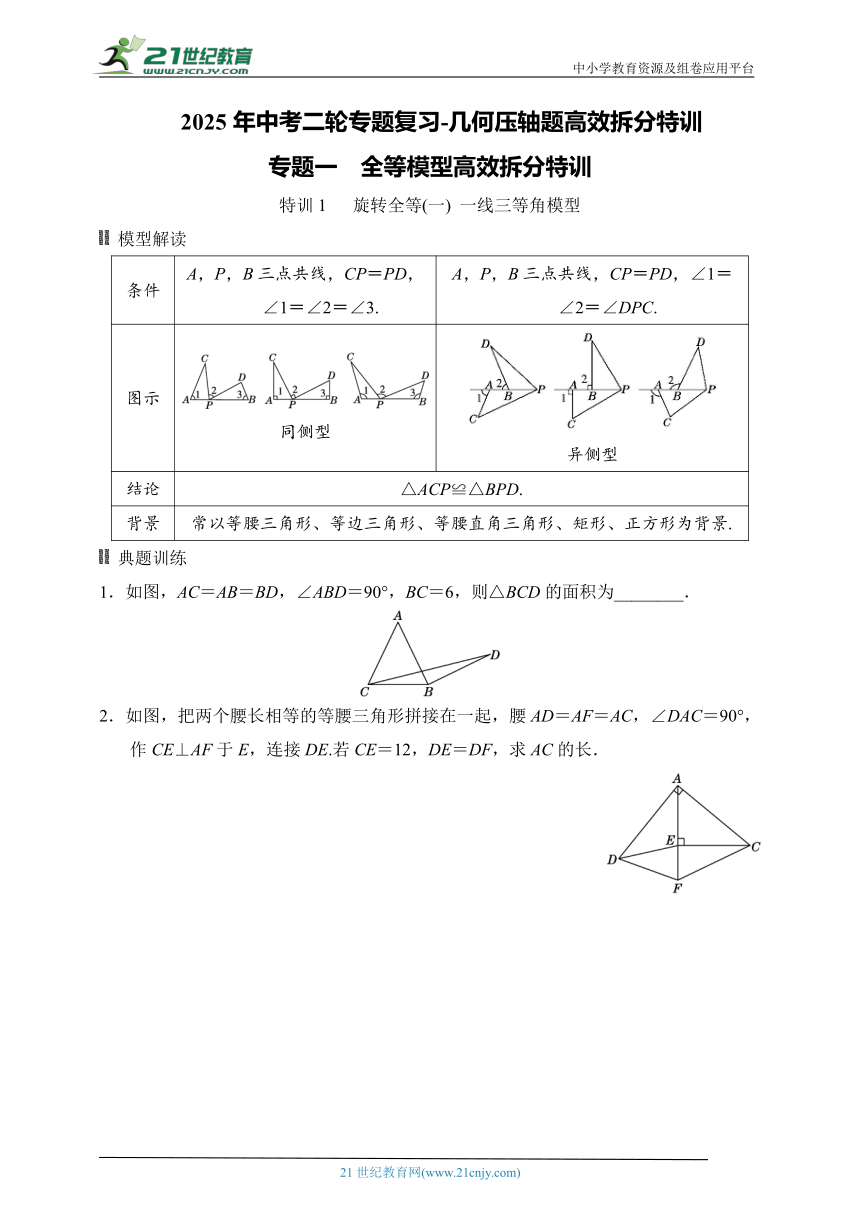
中小学教育资源及组卷应用平台 2025年中考二轮专题复习-几何压轴题高效拆分特训 专题一　全等模型高效拆分特训 INCLUDEPICTURE"标1.tif" INCLUDEPICTURE "D:\\课件\\中考福建数学\\标1.tif" \* MERGEFORMATINET 特训1　 旋转全等(一) 一线三等角模型INCLUDEPICTURE"标2.tif" INCLUDEPICTURE "D:\\课件\\中考福建数学\\标2.tif" \* MERGEFORMATINET INCLUDEPICTURE"条单.tif" INCLUDEPICTURE "D:\\课件\\中考福建数学\\条单.tif" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\庞建宇\\Desktop\\中考数学福建\\条单.tif" \* MERGEFORMATINET 模型解读 条件 A，P，B三点共线，CP＝PD，∠1＝∠2＝∠3. A，P，B三点共线，CP＝PD，∠1＝∠2＝∠DPC. 图示 INCLUDEPICTURE"SK1-1.tif" INCLUDEPICTURE "D:\\课件\\中考福建数学\\SK1-1.tif" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\庞建宇\\Desktop\\中考数学福建\\SK1-1.tif" \* MERGEFORMATINET 同侧型 异侧型 结论 △ACP≌△BPD. 背景 常以等腰三角形、等边三角形、等腰直角三角形、矩形、正方形为背景. INCLUDEPICTURE"条单.tif" INCLUDEPICTURE "D:\\课件\\中考福建数学\\条单.tif" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\庞建宇\\Desktop\\中考数学福建\\条单.tif" \* MERGEFORMATINET 典题训练 1．如图，AC＝AB＝BD，∠ABD＝90°，BC＝6，则△BCD的面积为_____． INCLUDEPICTURE"SK1-3.tif" INCLUDEPICTURE "D:\\课件\\中考福建数学\\SK1-3.tif" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\庞建宇\\Desktop\\中考数学福建\\SK1-3.tif" \* MERGEFORMATINET 2．如图，把两个腰长相等的等腰三角形拼接在一起，腰AD＝AF＝AC，∠DAC＝90°，作CE⊥AF于E，连接DE.若CE＝12，DE＝DF，求AC的长． INCLUDEPICTURE"SK1-4.tif" INCLUDEPICTURE "D:\\课件\\中考福建数学\\SK1-4.tif" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\庞建宇\\Desktop\\中考数学福建\\SK1-4.tif" \* MERGEFORMATINET INCLUDEPICTURE"标1.tif" INCLUDEPICTURE "D:\\课件\\中考福建数学\\标1.tif" \* MERGEFORMATINET 特训2　 旋转全等(二)手拉手模型INCLUDEPICTURE"标2.tif" INCLUDEPICTURE "D:\\课件\\中考福建数学\\标2.tif" \* MERGEFORMATINET INCLUDEPICTURE"条单.tif" INCLUDEPICTURE "D:\\课件\\中考福建数学\\条单.tif" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\庞建宇\\Desktop\\中考数学福建\\条单.tif" \* MERGEFORMATINET 模型解读 条件：如图，AB＝AC，AD＝AE，∠BAC＝∠DAE.INCLUDEPICTURE"SK1-5.tif" INCLUDEPICTURE "D:\\课件\\中考福建数学\\SK1-5.tif" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\庞建宇\\Desktop\\中考数学福建\\SK1-5.tif" \* MERGEFORMATINET 结论：△ACD≌△ABE. 顶角相等且顶点重合的两个等腰三角形→全等三角形. INCLUDEPICTURE"条单.tif" INCLUDEPICTURE "D:\\课件\\中考福建数学\\条单.tif" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\庞建宇\\Desktop\\中考数学福建\\条单.tif" \* MERGEFORMATINET 典题训练 【熟悉模型】 如图①，已知△ABC与△ADE都是等腰三角形，AB＝AC，AD＝AE，且∠BAC＝∠DAE，求证：BD＝CE； 【运用模型】 如图②，P为等边三角形ABC内一点，且PA∶PB∶PC＝3∶4∶5，求∠APB的度数．小明在解决此问题时，根据前面的“手拉手模型”，以BP为边构造等边三角形BPM，这样就有两个等边三角形共顶点B，然后连接CM，通过转化的思想求出了∠APB的度数，则∠APB的度数为_____； 【深化模型】 如图③，在四边形ABCD中，AD＝4，CD＝3，∠ABC＝∠ACB＝∠ADC＝45°，求BD的长． INCLUDEPICTURE"SK1-6.tif" INCLUDE ... ...