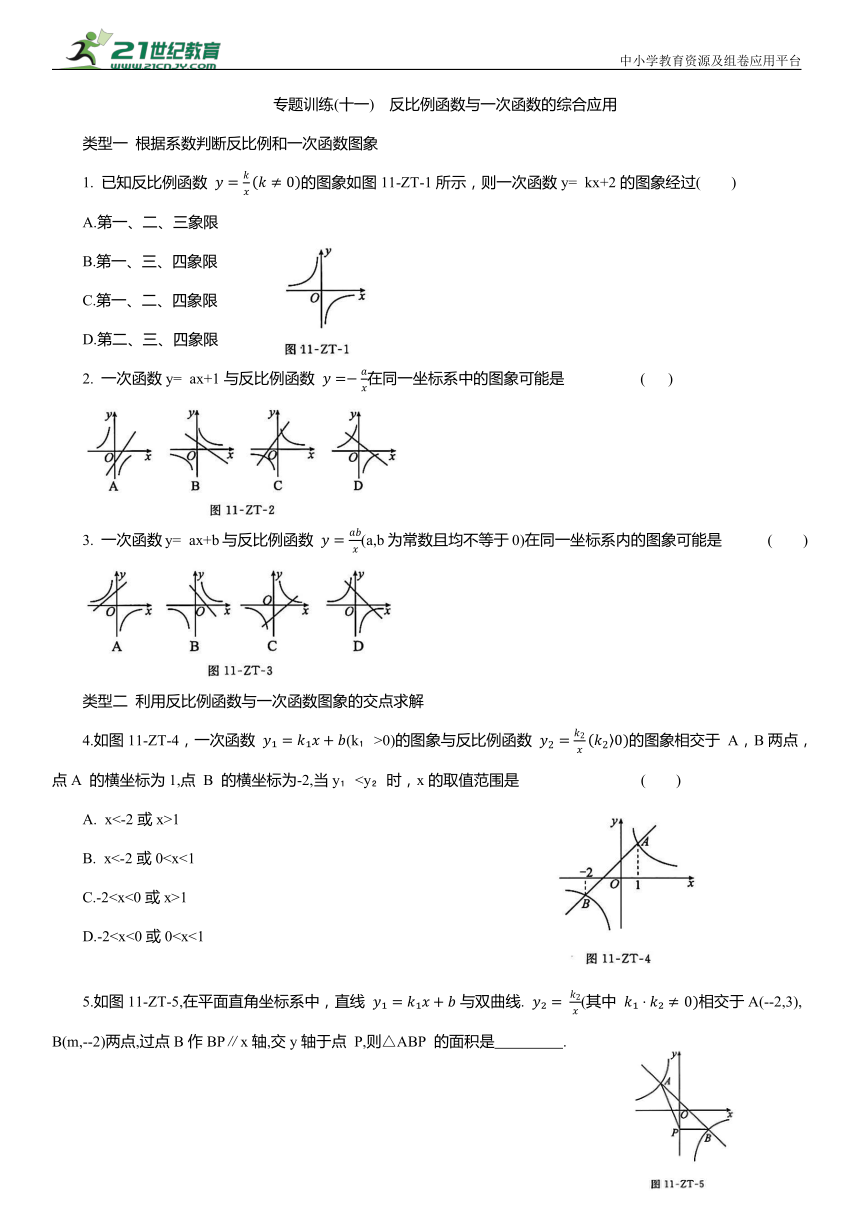
专题训练(十一) 反比例函数与一次函数的综合应用 练习（含答案）

专题训练(十一) 反比例函数与一次函数的综合应用 类型一 根据系数判断反比例和一次函数图象 1. 已知反比例函数 的图象如图11-ZT-1所示，则一次函数y= kx+2的图象经过( ) A.第一、二、三象限 B.第一、三、四象限 C.第一、二、四象限 D.第二、三、四象限 2. 一次函数y= ax+1与反比例函数 在同一坐标系中的图象可能是 ( ) 3. 一次函数y= ax+b与反比例函数 (a,b为常数且均不等于0)在同一坐标系内的图象可能是 ( ) 类型二 利用反比例函数与一次函数图象的交点求解 4.如图11-ZT-4，一次函数 (k >0)的图象与反比例函数 的图象相交于 A，B两点，点A 的横坐标为1,点 B 的横坐标为-2,当y 1 B. x<-2或01 D.-20时，关于x的不等式 的解集. 8. 如图11-ZT-8,一次函数. b(k≠0)与反比例函数 的图象交于A(4,1),.,B( ,a)两点. (1)求这两个函数的表达式； (2)根据图象，直接写出满足 时x的取值范围； (3)点 P 在线段AB 上,过点 P 作x 轴的垂线，垂足为 M，交反比例函数的图象于点 Q，若△POQ的面积为3，求点 P 的坐标. 中小学教育资源及组卷应用平台 1. C 2. B 3. D [解析] A项，∵一次函数图象经过第一、二、三象限,∴a>0,b>0,∴ab>0,∴,反比例函数 的图象经过第一、三象限，这与图形不符合，故A项不符合题意； B项，∵一次函数图象经过第一、二、四象限，∴a<0,b>0,∴ab<0,∴反比例函数 的图象经过第二、四象限，这与图形不符合，故B 项不符合题意； C项，∵一次函数图象经过第一、三、四象限，∴a>0,b<0,∴ab<0,∴反比例函数 的图象经过第二、四象限，这与图形不符合，故C 项不符合题意； D项，∵一次函数图象经过第一、二、四象限，∴a<0,b>0,∴ab<0,∴反比例函数 的图象经过第二、四象限，这与图形符合，故D 项符合题意. 故选 D. 4. B 5. [解析] ∵直线 与双曲线 kxx(其中 相交于A(--2,3),B(m,—2)两点, ∴双曲线的表达式为 ∵过点 B作BP∥x轴,交 y轴于点 P, 故答案为 6. 解：(1)将点 A 的坐标代入反比例函数表达式，得 ∴m=3.∴A(3,2). 将点 A 的坐标代入正比例函数表达式，得2=3k. (2)如图. ∴正比例函数值大于反比例函数值时x的取值范围为x>3或-30时，关于x的不等式 的解集是1y , 此时直线AB在反比例函数图象上方，此部分对应的x的取值范围为 即满足 时，x的取值范围为 x<4. (3)设点 P 的横坐标为p, 将x=p代入 可得 ∴P(p,-2p+9). 将x=p代入 可得 p=3, 整理得 解得 当p=2时,-2p+9=-2×2+9=5; 当 时， ∴点 P 的坐标为((2,5)或 ... ...