18.2特殊的平行四边形（含答案）

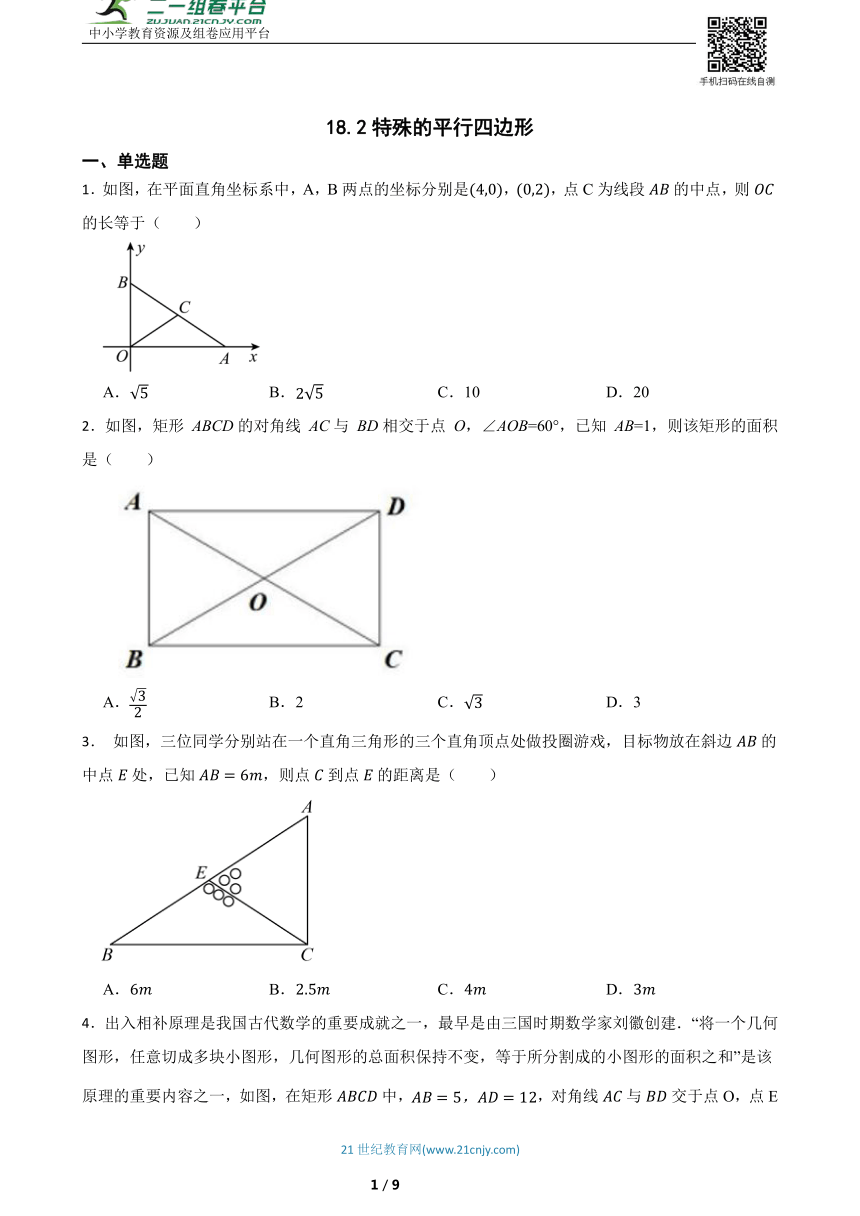
中小学教育资源及组卷应用平台 18.2特殊的平行四边形 一、单选题 1．如图，在平面直角坐标系中，A，B两点的坐标分别是，，点C为线段的中点，则的长等于（　　） A． B． C．10 D．20 2．如图，矩形 ABCD的对角线 AC与 BD相交于点 O，∠AOB=60°，已知 AB=1，则该矩形的面积是（　　） A． B．2 C． D．3 3． 如图，三位同学分别站在一个直角三角形的三个直角顶点处做投圈游戏，目标物放在斜边的中点处，已知，则点到点的距离是（　　） A． B． C． D． 4．出入相补原理是我国古代数学的重要成就之一，最早是由三国时期数学家刘徽创建．“将一个几何图形，任意切成多块小图形，几何图形的总面积保持不变，等于所分割成的小图形的面积之和”是该原理的重要内容之一，如图，在矩形中，，对角线与交于点O，点E为边上的一个动点，，，垂足分别为点F，G，则的值为（　　） A． B． C． D． 5．如图，在中，是斜边上的中线，若，则的度数为（　　） A． B． C． D． 6．如图，正方形ABCD中，AB＝4，M为AD的中点，延长MD至E，使ME＝MC，以DE为边作正方形DEFG，点G在边CD上，则DG的长为（　　） A．2﹣1 B．2﹣2 C．2+2 D．2﹣2 7．如图，在正方形中，点在边上，点在边上，连接、、，有，，若，求的长为（　　） A．8 B． C． D． 8．如图所示，面积为5的正方形的顶点在数轴上，且点表示的数为1，若点在数轴上点在点左侧，且，则点所表示的数为（　　） A． B． C． D． 9．如图，已知正方形的面积为4．它的两个顶点B，D是反比例函数（，）的图象上两点，若点D的坐标是，则的值为（　　） A．2 B． C． D． 10．如图，△ABC是边长为1的等边三角形，分别取AC，BC边的中点D，E，连接DE，作EF∥AC得到四边形EDAF，它的周长记作C1；分别取EF，BE的中点D1，E1，连接D1E1，作E1F1∥EF，得到四边形E1D1FF1，它的周长记作C2照此规律作下去，则C2019等于（　　） A． B． C． D． 二、填空题 11．若菱形ABCD的边长为13cm，对角线BD长10cm，则菱形ABCD的面积是　 　cm2. 12．如图，在平行四边形ABCD中，过AC中点O的直线分别交边BC，AD于点E，F，连接AE，CF．只需添加一个条件即可证明四边形AECF 是菱形，这个条件可以是_____（写出一个即可）． 13．将张宽为的小长方形按如图摆放在中，则的面积为　 　． 14．如图，在 中， ，点 、 、 分别是三边的中点，且 ，则 的长度是　 　. 15．如图，在一张长为7cm，宽为5cm的矩形纸片上，现要剪下一个腰长为4cm的等腰三角形（要求：等腰三角形的一个顶点与矩形的一个顶点重合，其余的两个顶点在矩形的边上），则剪下的等腰三角形的面积为　 　． 16．如图，在长方形中，，，E、F分别是、上的一点，，将沿翻折得到，连接．若是以为腰的等腰三角形，则　 　． 三、计算题 17．在直角三角形中，是边上的高， （1）求的面积； （2）求的长； （3）若的边上的中线是，求出的面积． 18．【问题背景】 如图1，数学实践课上，学习小组进行探究活动，老师要求大家对矩形进行如下操作：①分别以点为圆心，以大于的长度为半径作弧，两弧相交于点，，作直线交于点，连接；②将沿翻折，点的对应点落在点处，作射线交于点． 【问题提出】 在矩形中，，求线段的长． 【问题解决】 经过小组合作、探究、展示，其中的两个方案如下： 方案一：连接，如图2．经过推理、计算可求出线段的长； 方案二：将绕点旋转至处，如图3．经过推理、计算可求出线段的长． 请你任选其中一种方案求线段的长． 19．在菱形中，，点E、F分别为上一点． （1）如图1，当，时，直接写出三条线段和之间满足的等量关系式为_____； （2）当时， ①如图2，若，若，，求的长； ②如图3，E为中点，交于点G，交于点H，和交于点O，若，，，则_____． 四、 ... ...