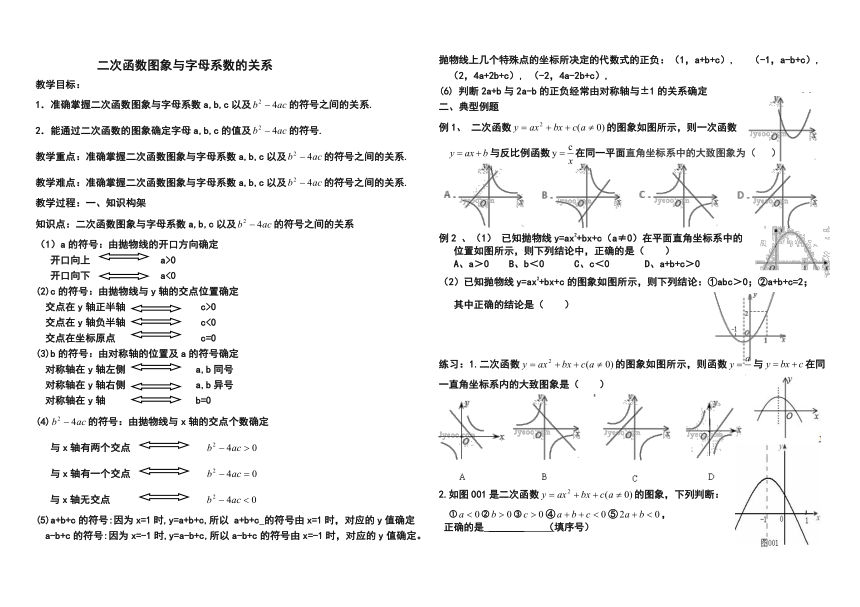
二次函数图象与字母系数的关系 教学目标: 1.准确掌握二次函数图象与字母系数a,b,c以及的符号之间的关系. 2.能通过二次函数的图象确定字母a,b,c的值及的符号. 教学重点:准确掌握二次函数图象与字母系数a,b,c以及的符号之间的关系. 教学难点:准确掌握二次函数图象与字母系数a,b,c以及的符号之间的关系. 教学过程:一、知识构架 知识点:二次函数图象与字母系数a,b,c以及的符号之间的关系 (1)a的符号:由抛物线的开口方向确定 开口向上 a>0 开口向下 a<0 (2)c的符号:由抛物线与y轴的交点位置确定 交点在y轴正半轴 c>0 交点在y轴负半轴 c<0 交点在坐标原点 c=0 (3)b的符号:由对称轴的位置及a的符号确定 对称轴在y轴左侧 a,b同号 对称轴在y轴右侧 a,b异号 对称轴在y轴 b=0 (4)的符号:由抛物线与x轴的交点个数确定 与x轴有两个交点 与x轴有一个交点 与x轴无交点 (5)a+b+c的符号:因为x=1时,y=a+b+c,所以 a+b+c 的符号由x=1时,对应的y值确定 a-b+c的符号:因为x=-1时,y=a-b+c,所以a-b+c的符号由x=-1时,对应的y值确定。抛物线上几个特殊点的坐标所决定的代数式的正负:(1,a+b+c), (-1,a-b+c), (2,4a+2b+c), (-2,4a-2b+c), (6) 判断2a+b与2a-b的正负经常由对称轴与±1的关系确定 二、典型例题 例1、 二次函数的图象如图所示,则一次函数 与反比例函数在同一平面直角坐标系中的大致图象为( ) 例2 、(1) 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的 位置如图所示,则下列结论中,正确的是( ) A、a>0 B、b<0 C、c<0 D、a+b+c>0 (2)已知抛物线y=ax2+bx+c的图象如图所示,则下列结论:①abc>0;②a+b+c=2; 其中正确的结论是( ) 练习:1.二次函数的图象如图所示,则函数与在同一直角坐标系内的大致图象是( ) 2.如图001是二次函数的图象,下列判断: ④⑤, 正确的是 _____ (填序号) 3.如图002是二次函数的图象,下列判断: ④ ⑤ 其中错误的有 (填序号) 三、课堂小结:谈谈你的收获 四、课下作业 1.函数的图象经过地一、二、三象限,那么函数的图像大致是( ) 2.二次函数的大致图象如图,下列说法错误的是( ) A.函数有最小值 B.对称轴是直线 C.当,y随x的增大而减小 D.当-1<x<2时,y>0 (2题图) (3题图) (4题图) 3.如图所示抛物线是二次函数的图象,给出下列结论:①abc>0;②b+2a=0;③抛物线与x轴的另一个交点为(4,0);④a+c>b;⑤3a+c<0. 其中正确的结论有( ) A.5个 B.4个 C.3个 D.2个 4.如图是二次函数的图象一部分,x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c=-9a;④若(-3,y1),(,y2)是抛物线上两点,则y1>y2,其中正确的是( ) A、①②③ B、①③④ C、①②④ D、②③④ 5.如图003是二次函数的图象一部分,则以下正确的有; ②的两根分别为-3和1;④⑤ 其中正确的有 (填序号) 6.如图004是二次函数的图象,有下列5个结论:④⑤ ⑥;你认为其中正确的有 (填序号) 7.抛物线的顶点为D(-1,2),与x轴的一个点A在点(-3,0)和(-2,0)之间,其部分图象如图所示,则以下结论:①b -4ac<0②a+b+c<0③c-a=2 ④方程ax +bx+c-2=0有两个不相等的实数根.正确的有()个 A.1个 B.2个 C.3个 D.4个 ... ...
~~ 您好,已阅读到文档的结尾了 ~~