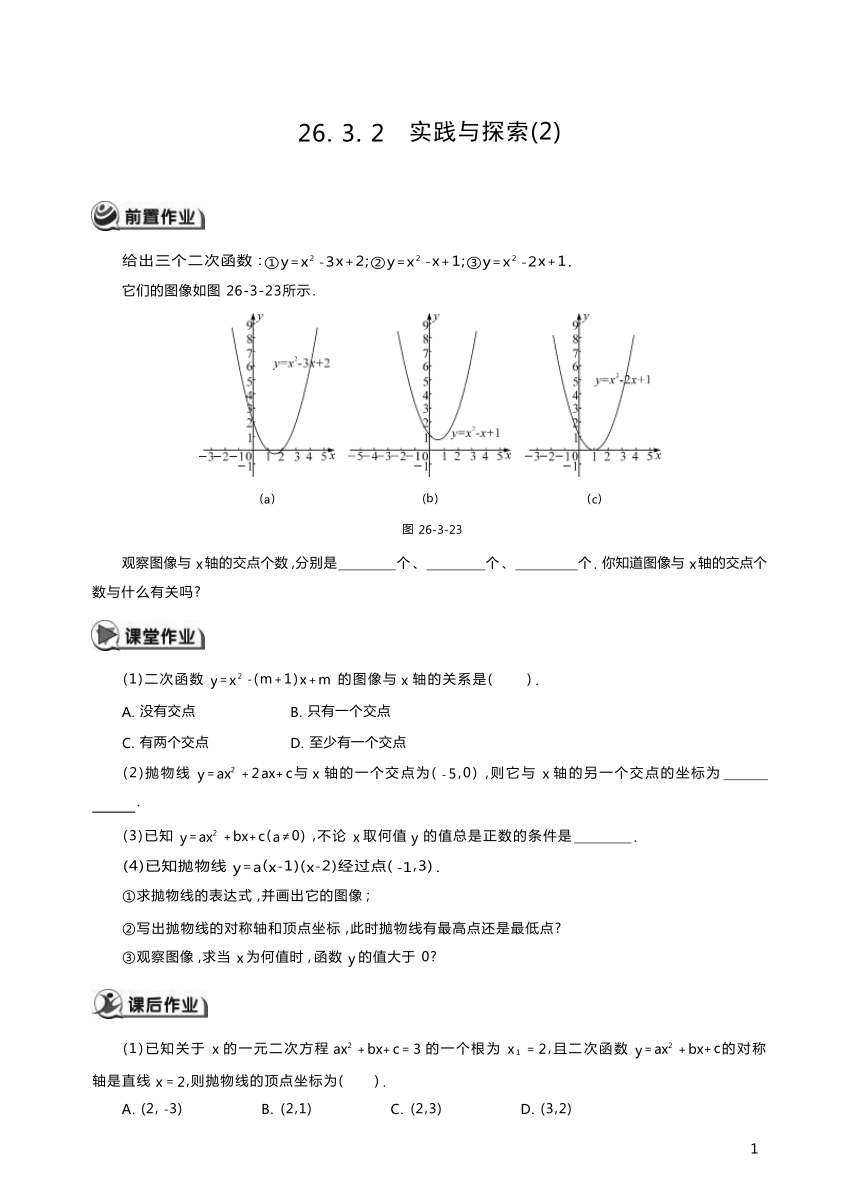
26. 3. 2 实践与探索(2) 给出三个二次函数 : ①y=x2 -3x+2;②y=x2 -x+1;③y=x2 -2x+1. 它们的图像如图 26-3-23所示 . (a) (b) (c) 图 26-3-23 观察图像与 x 轴的交点个数 ,分别是 个 、 个 、 个 . 你知道图像与 x 轴的交点个 数与什么有关吗 (1)二次函数 y=x2 -(m+1)x+m 的图像与 x 轴的关系是( ) . A. 没有交点 B. 只有一个交点 C. 有两个交点 D. 至少有一个交点 (2)抛物线 y=ax2 +2ax+c与 x 轴的一个交点为( -5,0) ,则它与 x 轴的另一个交点的坐标为 . (3)已知 y=ax2 +bx+c(a≠0) ,不论 x 取何值 y 的值总是正数的条件是 . (4)已知抛物线 y=a(x-1)(x-2)经过点( -1,3) . ①求抛物线的表达式 ,并画出它的图像 ; ②写出抛物线的对称轴和顶点坐标 ,此时抛物线有最高点还是最低点 ③观察图像 ,求当 x 为何值时 , 函数 y 的值大于 0 (1)已知关于 x 的一元二次方程 ax2 +bx+c= 3 的一个根为 x1 = 2,且二次函数 y=ax2 +bx+c的对称 轴是直线 x = 2,则抛物线的顶点坐标为( ) . A. (2, -3) B. (2,1) C. (2,3) D. (3,2) 1 (2)若抛物线 y=ax2 +bx+c的所有点都在 x 轴下方 ,则必有 ( ) . A. a<0. b2 -4ac>0 B. a>0,b2 -4ac>0 C. a<0,b2 -4ac<0 D. a>0,b2 -4ac<0 (3)二次函数 y= x2 - 4x + 3 与 x 轴 有 两 个 交 点 , 即 方 程 x2 - 4x + 3 = 0 有 的 实 数 根 ,x1 = ,x2 = . (4)已知抛物线 y=ax2 +bx+c的图像与 x 轴有两个交点,那么一元二次方程 ax2 +bx+c= 0 的根的情 况是 . (5)二次函数 y=ax2 +bx+c(a≠0,a,b,c是常数)中 , 自变量 x 与函数 y 的对应值如下表所示 . x … -1 ( 1 2 ) 0 1 2 1 2 3 … y … -2 1 - 4 1 7 4 2 1 1 - 4 -2 … ①判断二次函数图像的开口方向 ,并写出它的顶点坐标 ; ②一元二次方程 ax2 +bx+c= 0(a≠0,a,b,c是常数)的两个根 x1 ,x2 的取值范围是( ) . C. -
~~ 您好,已阅读到文档的结尾了 ~~