第 27章 圆 评估检测题(B卷) （无答案）2024-2025学年九年级下册数学华师版

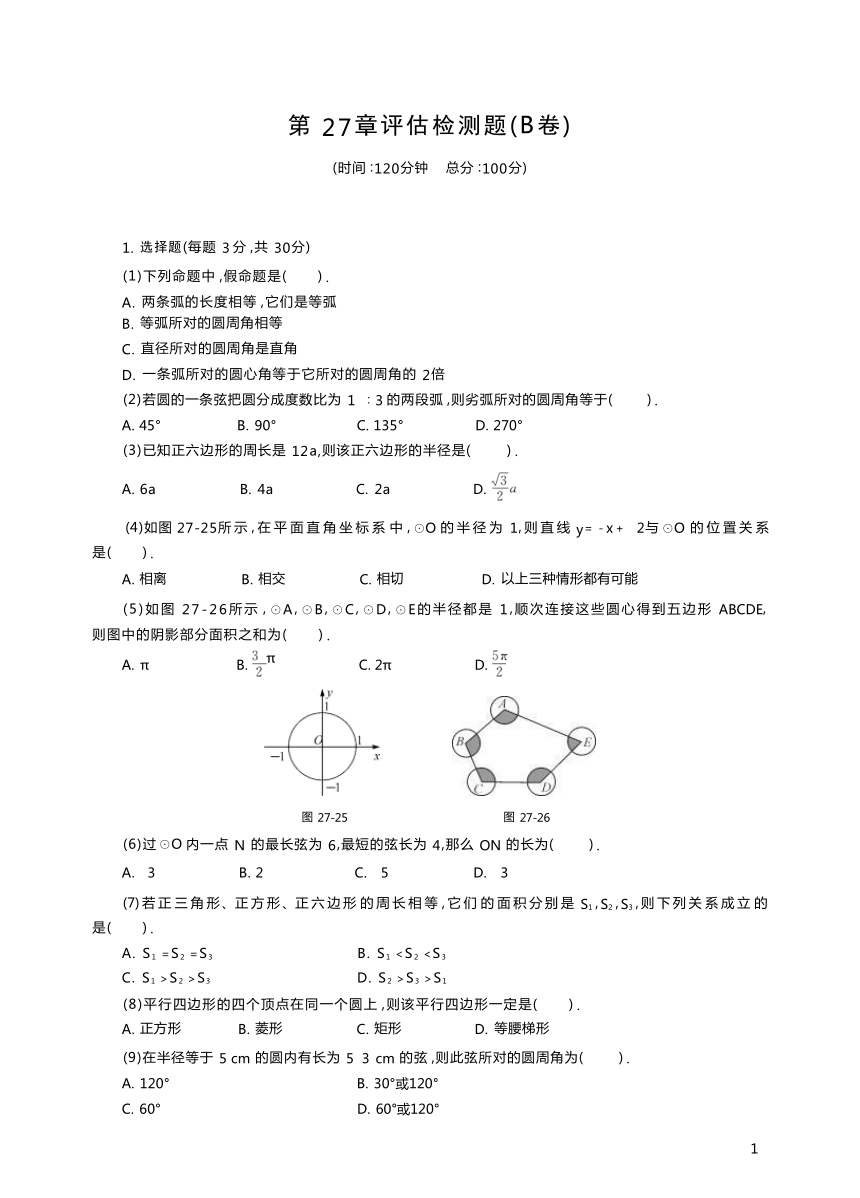
第 27章评估检测题(B卷) (时间 :120分钟 总分 :100分) 1. 选择题(每题 3 分 ,共 30分) (1)下列命题中 ,假命题是( ) . A. 两条弧的长度相等 ,它们是等弧 B. 等弧所对的圆周角相等 C. 直径所对的圆周角是直角 D. 一条弧所对的圆心角等于它所对的圆周角的 2倍 (2)若圆的一条弦把圆分成度数比为 1 ∶3 的两段弧 ,则劣弧所对的圆周角等于( ) . A. 45° B. 90° C. 135° D. 270° (3)已知正六边形的周长是 12a,则该正六边形的半径是( ) . A. 6a B. 4a C. 2a D. (4)如图 27-25所 示 , 在 平 面 直 角 坐 标 系 中 , ☉O 的 半 径 为 1, 则 直 线 y= - x + 2与 ☉O 的 位 置 关 系 是( ) . A. 相离 B. 相交 C. 相切 D. 以上三种情形都有可能 (5)如图 27-26所示 , ☉A, ☉B, ☉C, ☉D, ☉E的半径都是 1,顺次连接这些圆心得到五边形 ABCDE, 则图中的阴影部分面积之和为( ) . A. π B. π C. 2π D. 图 27-25 图 27-26 (6)过 ☉O 内一点 N 的最长弦为 6,最短的弦长为 4,那么 ON 的长为( ) . A. 3 B. 2 C. 5 D. 3 (7) 若 正 三 角 形 、正 方 形 、正 六 边 形 的 周 长 相 等 , 它 们 的 面 积 分 别 是 S1 , S2 , S3 , 则 下 列 关 系 成 立 的 是( ) . A. S1 =S2 =S3 B. S1 S2 >S3 D. S2 >S3 >S1 (8)平行四边形的四个顶点在同一个圆上 ,则该平行四边形一定是( ) . A. 正方形 B. 菱形 C. 矩形 D. 等腰梯形 (9)在半径等于 5 cm 的圆内有长为 5 3 cm 的弦 ,则此弦所对的圆周角为( ) . A. 120° B. 30°或120° C. 60° D. 60°或120° 1 (10)如图 27-27所示 , ☉O 是 △ABC的内切圆 , 切点分 别 是 点 D,E、F, 已 知 ∠A= 100°, ∠C= 30°, 则 ∠DFE的度数为( ) . 图 27-27 A. 55° B. 60° C. 65° D. 70° 2. 填空题(每题 3 分 ,共 30分) (1)如图 27-28所示 , 已知 AB为 ☉O的直径 ,AB⊥CD,垂足为点 E, 由图你还能知道哪些正确的结论 请把它们一一写出来 . . (2)如图 27-29所示 ,AB是 ☉O的直径 ,C为圆上一点 , ∠A= 60°,OD⊥BC,D 为垂足 ,且 OD= 10,则 2 AB= ,BC= . ( ︵ ︵ ︵ )(3)如图 27-30所示 , 已知 ☉O中 ,AB=BC,且AB ∶—= 3 ∶4,则 ∠AOC= . 图 27-28 图 27-29 图 27-30 (4)如图 27-31所示 ,在条件 : ①∠COA= ∠AOD= 60°; ②AC=AD=OA;③点 E 分别是 AO,CD 的中 点 ; ④OA⊥CD,且 ∠ACO= 60°中 ,能推出四边形 OCAD 是菱形的条件有 个 . (5)为了改善市区人民的生活环境 ,某市建设污水管网工程 ,某圆柱形水管的直径为 100 cm ,截面如图 27-32所示 ,若管内的污水的面宽 AB= 60 cm ,则污水的最大深度为 . 图 27-31 图 27-32 (6) ☉O的直径为 11 cm , 圆心到一条直线的距离为 5 cm ,那么这条直线和圆的位置关系是 ;若 圆心到一直线的距离为 5.5 cm ,那么这条直线和圆的位置关系是 . (7)若两圆相切 , 圆心距为 8 cm ,其中一个圆的半径为 12 cm ,则另一个圆的半径为 . (8)正五边形的一个中心角的度数为 . (9)已知 ☉O1 和 ☉O2 的半径分别为 2 和 3,如果它们既不相交又不相切 ,那么它们的圆心距 d 的取值 范围是 . (10)已知 在 同 一 平 面 内 圆 锥 两 母 线 在 顶 点 处 最 大 的 夹 角为 60°, 母 线 长 为 8, 则 圆 锥 的 侧 面 积 为 . 3. 解答题(共 40分) (1)如图 27-33所示 , 已知 △ABC中 , ∠C= 90°,AC= 3,BC= 4, 已点 C为圆心作 ☉C,半径为 r. (5分) ①当 r取什么值时,点 A,B 在 ☉C外 ②当 r取什么值时,点 A 在 ☉C内,点 B 在 ☉C外 图 27-33 (2)如图 27-34所示 ,两个同心圆 ,作一条直线交大圆于点 A,B,交小圆于点 C,D,AC与 BD 有何关系 请说明理由 . (5分) 图 27-34 (3)如图 27-35所示 ,PA,PB 是 ☉O 的两条切线 ,A,B 是切点,AC 是 ☉O的直径 , ∠BAC= 35°,求 ∠P 的度数 . (5分) 图 27-35 (4)如图 ... ...