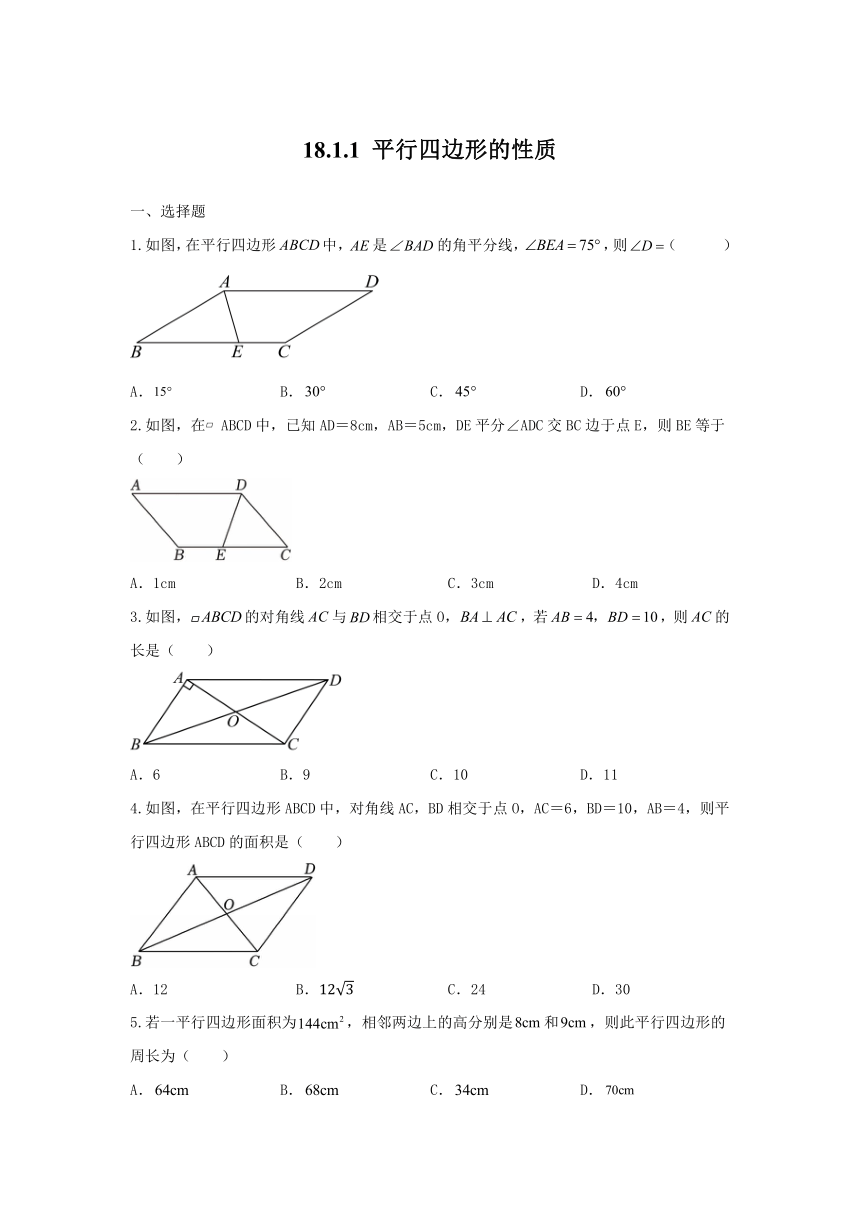
18.1.1 平行四边形的性质 一、选择题 1.如图,在平行四边形中,是的角平分线,,则( ) A. B. C. D. 2.如图,在 ABCD中,已知AD=8cm,AB=5cm,DE平分∠ADC交BC边于点E,则BE等于( ) A.1cm B.2cm C.3cm D.4cm 3.如图,的对角线与相交于点O,,若,则的长是( ) A.6 B.9 C.10 D.11 4.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,AC=6,BD=10,AB=4,则平行四边形ABCD的面积是( ) A.12 B. C.24 D.30 5.若一平行四边形面积为,相邻两边上的高分别是和,则此平行四边形的周长为( ) A. B. C. D. 6.如图,在平行四边形ABCD中,AC与BD相交于点O,则下列结论不一定成立的是( ) A.AO=DO B.CD=AB C.∠BAD=∠BCD D.ADBC 7.已知中,∠A=55°,分别以点B,点C为圆心,以大于的长为半径画弧,分别交于点M,N,作直线交于点E,则的度数为( ) A.55° B.60° C.65° D.70° 8.在平面直角坐标系中, ABCD的顶点A、B、D的坐标分别是(0,0),(4,0),(2,3),则顶点C的坐标是( ) A.(4,3) B.(5,3) C.(3,6) D.(6,3) 二、填空题 9.如图,在平行四边形中,平分交边于点,,则的度数是 . 10.在平面直角坐标系中, ABCD的顶点A、B、C的坐标分别是(0,2)、(﹣3,﹣4)、(2,﹣4),则顶点D的坐标是 . 11.如图,在平行四边形中,对角线相交于点O.已知两条对角线长的和为,长为.则的周长为 . 12.如图,已知AB∥CD,O为∠CAB、∠ACD的角平分线的交点,OE⊥AC于E,且OE=1.5,则两平行线AB、CD间的距离等于 . 13.如图,在平面直角坐标系中,平行四边形的坐标分别为,、、,若P是x轴上的一动点,若点A关于的对称点为,则的最小值为 ,的最大值为 . 解答题 14.如图,在 ABCD中,AE⊥CD,AF⊥BC,垂足分别为E,F,∠EAF=60°,CE=1,CF=4.求 ABCD各边长. 15.如图,已知四边形均为平行四边形,相交于点O,且在同一条直线上,,试求的长. 16.如图所示,在 ABCD中,AD⊥BD,AD=4,OD=3. (1)求△COD的周长; (2)直接写出 ABCD的面积. 17.如图,的两条对角线、相交于点,点、分别是、上的中点.连接、.求证:. 18.如图,在平行四边形中,对角线,相交于点,,点在线段上,且. 求证:; 若,分别是,的中点,且, 求证:是等腰三角形; 当时,求平行四边形的面积. 答案 1.B 2.C 3.A 4.C 5.B 6.A 7.D 8.D 9.110 10.5,2 11.15 12.3 13. / / 14.解:∵AE⊥CD,AF⊥BC,∠EAF=60°, ∴∠C=360°﹣90°﹣90°﹣60°=120°, ∵四边形ABCD是平行四边形, ∴AB∥CD,AD∥BC,∠B=∠D=180°﹣∠C=60°, ∴在Rt△BAF中,∠BAF=30°, ∴AB=2BF, 设BF=x,则AB=CD=2x,BC=BF+CF=x+4, ∵DE=CD﹣CE=2x﹣1, ∵在Rt△ADE中,∠DAE=30°, ∴AD=2DE, ∴x+4=2(2x﹣1), 解得:x=2, ∴AB=CD=4,BC=AD=6. 15.解:∵四边形均为平行四边形, ∴, ∴, ∴, 在△ADE与△CBF中,, ∴△ADE≌△CBF ∴, ∵, ∴. 16.解:(1)∵四边形ABCD是平行四边形, ∴BD=2OD=2×3=6, ∵AD⊥BD,AD=4, ∴AB2,OA5, ∴CD=AB=2,OC=OA=5, ∴△COD的周长为:OD+OC+CD=8+2; (2)S ABCD=AD BD=4×6=24. 17.证明:∵四边形是平行四边形, ∴,,, ∴, ∵点、分别是、上的中点, ∵,, ∴, ∴ 即, 在△ADE和△CBF中, , ∴, ∴. 18.证明:四边形是平行四边形, ,,, , , , , 是中点, , ; 证明:, 是等腰三角形, 是中点, , , 为中点, , 四边形是平行四边形, , 、分别是、的中点, , , 是等腰三角形; 由得, , , 是的中点, , 设,则, , 在中,, , 即, 解得, ... ...
~~ 您好,已阅读到文档的结尾了 ~~

