2025年 九年级数学中考二轮复习 二次函数常考考点分类 解答题专题提升训练（含答案）

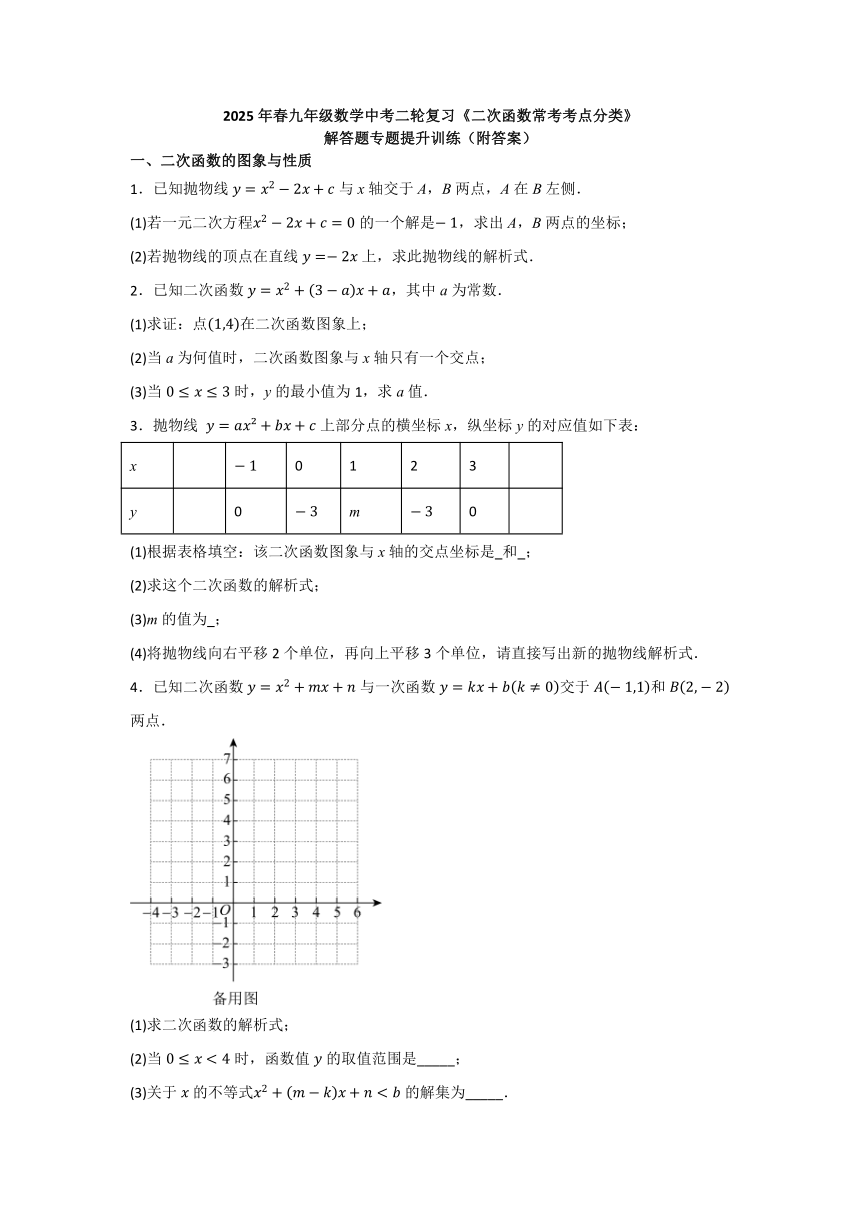
2025年春九年级数学中考二轮复习《二次函数常考考点分类》 解答题专题提升训练（附答案） 一、二次函数的图象与性质 1．已知抛物线与x轴交于A，B两点，A在B左侧． (1)若一元二次方程的一个解是，求出A，B两点的坐标； (2)若抛物线的顶点在直线上，求此抛物线的解析式． 2．已知二次函数，其中a为常数． (1)求证：点在二次函数图象上； (2)当a为何值时，二次函数图象与x轴只有一个交点； (3)当时，y的最小值为1，求a值． 3．抛物线 上部分点的横坐标x，纵坐标y的对应值如下表： x 0 1 2 3 y 0 m 0 (1)根据表格填空：该二次函数图象与x轴的交点坐标是 和 ； (2)求这个二次函数的解析式； (3)m的值为 ； (4)将抛物线向右平移2个单位，再向上平移3个单位，请直接写出新的抛物线解析式． 4．已知二次函数与一次函数交于和两点． (1)求二次函数的解析式； (2)当时，函数值的取值范围是_____； (3)关于的不等式的解集为_____． 5．已知二次函数的图象经过和两点，如图所示． (1)求这个二次函数的解析式和它的图象的顶点坐标； (2)求该二次函数在范围内的最大值与最小值； (3)请直接写出不等式的解集． 6．利用抛物线图象图象解决下列问题： (1)写出方程的根为_____； (2)写出方程的根为_____； (3)写出方程的根为_____； (4)写出不等式的解集为_____； (5)写出方程有两个不等实数根，则m的取值范围为_____； (6)观察可得： _____． 7．已知抛物线，顶点为点，与轴交于点，与轴交于点． (1)求顶点坐标； (2)求的面积； (3)点是直线上方抛物线上的点且不同于顶点，是否存在点，使得和面积相等？若存在，直接写出点的坐标，若不存在，请说明理由？ 二、实际问题与二次函数 8．芯片行业是制约我国工业发展的主要技术之一．经过大量科研、技术人员艰苦攻关，我国芯片有了新突破．某芯片实现国产化后，芯片价格大幅下降．原来每片芯片的单价为元，准备进行两次降价，如果每次降价的百分率都为，经过两次降价后的价格为（元）． (1)求与之间的函数关系式； (2)如果该芯片经过两次降价后每片芯片单价为元，求每次降价的百分率． 9．如图，热爱生活的兰兰想对自家阳台上的栏杆进行装饰，把每根柱子下段涂色．测量发现长为，栏杆被12根柱子等分成13份，使每根柱子上涂有颜色部分的顶端及点A，B所在曲线呈抛物线形（柱子宽度忽略不计），且左起第4根柱子涂色部分的高度．请完成下列任务： (1)求左起第一根柱子涂色部分的高度； (2)爸爸想了想说，有两根相邻的柱子涂色部分的高度相差，请你帮兰兰求出这两根柱子分别是左起第几根． 10．已知，如图中，，，，点D在边上，交于点E． (1)当时，求线段的长； (2)已知，点G，H在边上且四边形是矩形，当四边形的面积最大时，判断点D在线段上的位置？ (3)已知点M是边上的一动点，若是等腰直角三角形，请直接写出线段的长_____． 11．消防演练中，水枪喷出的水流是如图的一条抛物线，水流的高度y（单位：m）与离高楼的水平距离x（单位：m）之间具有二次函数关系．从地面离高楼水平距离的点A处，水枪喷出的水流在与高楼的水平距离为处达到最高，高度为，水流落到高楼的点B处． (1)求水流抛物线的解析式； (2)已知高楼的点C处，离地面的高度是． ①若在地面点A处竖直升高水枪的高度，使水枪喷出的水流恰好落到高楼的点C处，求水枪竖直升高的高度； ②若在地面点A处水平移动水枪的位置，使水枪喷出的水流恰好落到高楼的点C处，直接写出水枪水平移动的方法． 12．被推出的铅球的运动路径可看作抛物线的一部分，如图，以地面水平方向为x轴，出手点到地面的垂线为y轴，建立平面直角坐标系．小明第一次推铅球时，铅球出手时离地面的高度为，铅球落地时，离出手点的水平距离是，铅球运行的水平距离为时达到最大高度 ... ...