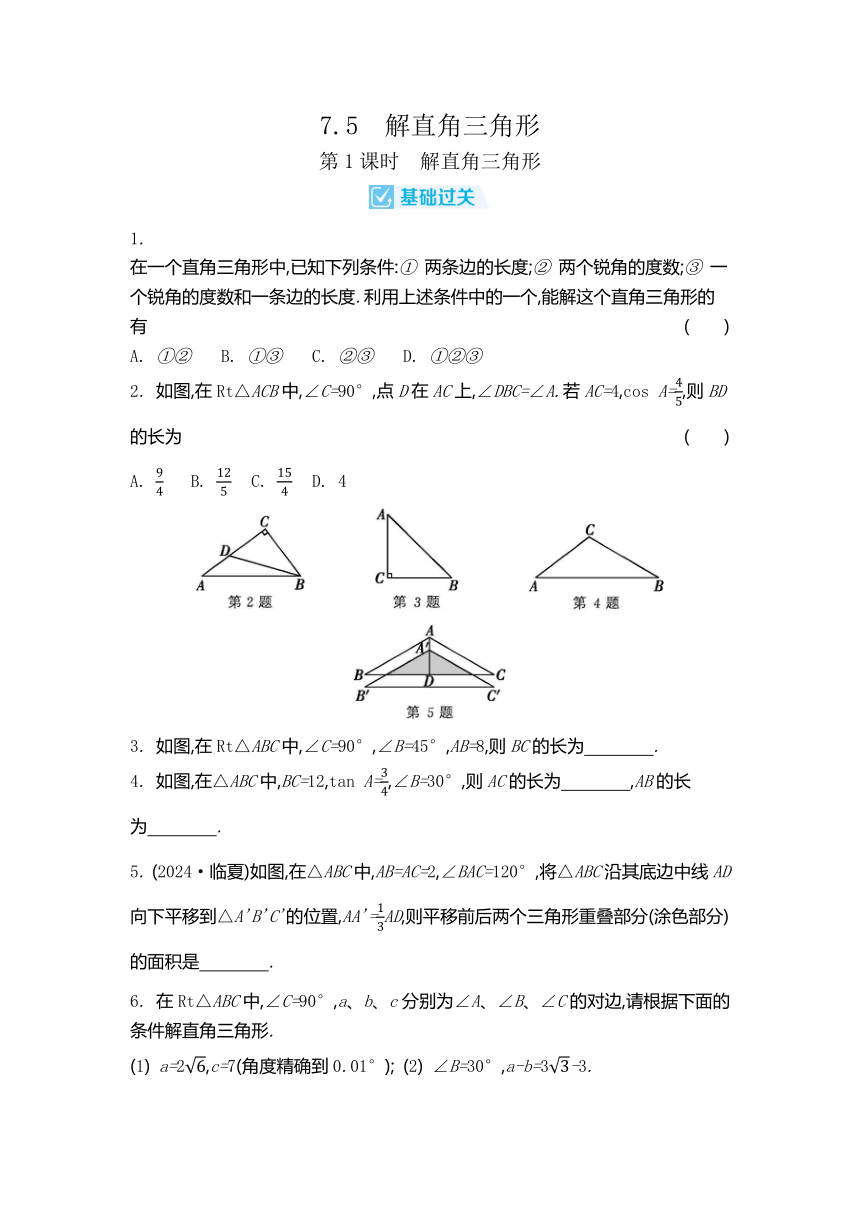
7.5 解直角三角形 第1课时 解直角三角形 1. 在一个直角三角形中,已知下列条件:① 两条边的长度;② 两个锐角的度数;③ 一个锐角的度数和一条边的长度.利用上述条件中的一个,能解这个直角三角形的有 ( ) A. ①② B. ①③ C. ②③ D. ①②③ 2. 如图,在Rt△ACB中,∠C=90°,点D在AC上,∠DBC=∠A.若AC=4,cos A=,则BD的长为 ( ) A. B. C. D. 4 3. 如图,在Rt△ABC中,∠C=90°,∠B=45°,AB=8,则BC的长为 . 4. 如图,在△ABC中,BC=12,tan A=,∠B=30°,则AC的长为 ,AB的长为 . 5. (2024·临夏)如图,在△ABC中,AB=AC=2,∠BAC=120°,将△ABC沿其底边中线AD向下平移到△A'B'C'的位置,AA'=AD,则平移前后两个三角形重叠部分(涂色部分)的面积是 . 6. 在Rt△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,请根据下面的条件解直角三角形. (1) a=2,c=7(角度精确到0.01°); (2) ∠B=30°,a-b=3-3. 第7题 7. (2023·凉山)如图,在☉O中,OA⊥BC,∠ADB=30°,BC=2,则OC的长为 ( ) A. 1 B. 2 C. 2 D. 4 8. 如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为 ( ) A. B. 2 C. D. 3 9. 如图,在四边形ABCD中,∠A=∠ABC=90°,DB平分∠ADC.若AD=1,CD=3,则sin∠ABD的值为 . 10. (2024·南充)如图,在矩形ABCD中,E为边AD上一点,∠ABE=30°,将△ABE沿BE折叠得△FBE,连接CF、DF,若CF平分∠BCD,AB=2,则DF的长为 . 11. (2024·长沙)如图,在菱形ABCD中,AB=6,∠B=30°,E是边BC上的动点,连接AE、DE,过点A作AF⊥DE于点F.设DE=x,AF=y,求y与x之间的函数表达式(不考虑自变量x的取值范围). 第11题 12. (2024·广元)如图,在△ABC中,AC=BC,∠ACB=90°,☉O经过A、C两点,交AB于点D,CO的延长线交AB于点F,DE∥CF交BC于点E,连接CD. (1) 求证:DE为☉O的切线; (2) 若AC=4,tan∠CFD=2,求☉O的半径. 第12题 第2课时 构造直角三角形解题 1. 正三角形的内切圆半径、外接圆半径和高的比为 ( ) A. 1∶2∶3 B. 2∶3∶4 C. 1∶∶ D. 1∶∶2 2. (2023·益阳)如图,在平面直角坐标系中,有点A(0,1)、B(4,1)、C(5,6),则sin∠BAC的值为 ( ) A. B. C. D. 3. 如图所示为墙壁上在l1、l2两条平行线间边长为a的正方形瓷砖,该瓷砖与平行线的较大夹角的度数为β,则两条平行线间的距离为 ( ) A. asinβ B. asinβ+acosβ C. 2acosβ D. asinβ-acosβ 4. 如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是 . 5. (2024·达州)如图,由8个全等的菱形组成的网格中,每个菱形的边长均为2,∠ABD=120°,其中点A、B、C都在格点上,则tan∠BCD的值为 . 6. 如图,在△ABC中,BC=+,∠C=45°,AB=AC,求AC的长. 第6题 7. 若正方形的外接圆半径为2,则其内切圆半径为 ( ) A. B. 2 C. D. 1 第8题 8. 如图,△ABC内接于☉O.若BC=2,tanA=,则☉O的直径为 ( ) A. 7 B. C. D. 5 9. 如图,△ABC内接于☉O,AO=2,BC=2,则∠BAC的度数为 . 10. 把两把同样大的含45°角的三角尺按如图所示的方式放置,其中一把三角尺的锐角顶点与另一把三角尺的直角顶点重合于点A,且另三个锐角顶点B、C、D在同一条直线上.若AB=,则CD的长为 . 11. (2024·贵州)如图,在菱形ABCD中,E、F分别是BC、CD的中点,连接AE、AF.如果sin∠EAF=,AE=5,那么AB的长为 . 12. 如图,在正方形方格纸中,每个小正方形的边长都为1,点A、B、C、D都在格点处,BA与CD相交于点P,则cos∠APC的值为 . 13. 如图,△ABC的顶点都在小正方形网格的格点上,求∠BAC的三个三角函数值. 第 ... ...
~~ 您好,已阅读到文档的结尾了 ~~

