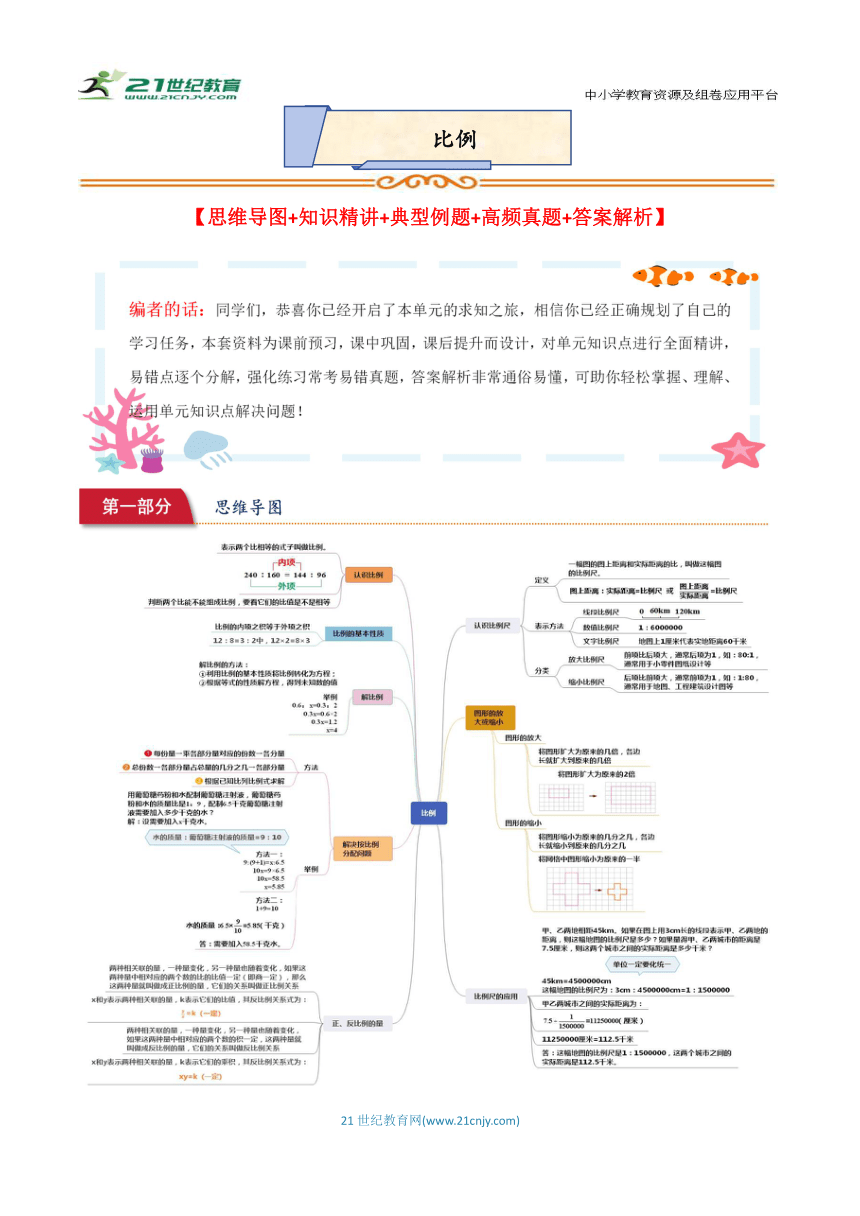
【思维导图+知识精讲+典型例题+高频真题+答案解析】 例题1:在比例尺是的图纸上,画一个边长是4厘米的正方形草坪,草坪的实际周长是多少米?实际面积是多少公顷? 【答案】见试题解答内容 【分析】先依据“图上距离÷比例尺=实际距离”求出正方形的边长的实际长度,进而依据正方形的周长=边长×4和面积=边长×边长即可得解,注意单位换算. 【解答】解:420000(cm) 20000cm=200 m 周长为200×4=800 (m) 面积为 200×200=40000(m2) 40000m2=4公顷 答:草坪的实际周长是800米,实际面积是4公顷. 【点评】此题主要考查图上距离、实际距离和比例尺的关系,以及正方形的周长面积的计算方法. 例题2:一个房间,用边长5dm的方砖铺地,需要128块,如果改成用边长8dm的方砖铺地,需要多少块? 【答案】50块。 【分析】房间的面积一定,方砖的面积与块数成反比例,解决此题,首先根据方砖的边长得求出方砖的面积。据此列出比例解答即可。 【解答】解:设需要x块。 82x=52×128 64x÷64=3200÷64 x=50 答:需要50块。 【点评】根据问题中的不变量找出两种相关联的量,并判断这两种相关联的量成什么比例关系,根据正、反比例关系式列出相应的方程并求解。 例题3:一个长方形的篮球场,长40米,宽30米,请你用的比例尺画出篮球场的平面图.(先计算,再画图) 【答案】见试题解答内容 【分析】篮球场的长和宽的实际长度以及比例尺已知,依据“图上距离=实际距离×比例尺”即可求出篮球场长和宽的图上距离,进而就可以画出篮球场的平面图. 【解答】解:40米=4000厘米,30米=3000厘米 40002(厘米) 30001.5(厘米) 【点评】此题主要考查图上距离、实际距离和比例尺的关系. 例题4:世界上最长的跨海大桥﹣﹣杭州湾跨海大桥,在比例尺1:400000的地图上量得它的长度是9cm.杭州湾跨海大桥的实际长度是多少千米? 【答案】见试题解答内容 【分析】要求杭州湾跨海大桥的实际长度是多少千米,根据“图上距离÷比例尺=实际距离”,代入数值,计算即可. 【解答】解:93600000(厘米) 3600000厘米=36千米. 答:杭州湾跨海大桥的实际长度是36千米. 【点评】此题有计算公式可用,根据图上距离、比例尺和实际距离三者的关系,进行分析解答即可得出结论. 例题5:在一幅地图上,量得广州到东莞的图上距离是4厘米,广州到东莞的实际距离大约是50千米.求这幅地图的比例尺是多少? 【答案】见试题解答内容 【分析】已知图上距离、实际距离,求比例尺,用比例尺=图上距离:实际距离,统一单位代入即可解决问题. 【解答】解:4厘米:50千米 =4厘米:5000000厘米 =1:1250000 答:这幅地图的比例尺是1:1250000. 【点评】本题考查了考查了比例尺的概念,图上距离、实际距离、比例尺三者之间的关系. 1.比例的意义和基本性质 【知识点归纳】 比例的意义:表示两个比相等的式子,叫做比例. 组成比例的四个数,叫做比例的项. 组成比例两端的两项叫做外项,中间的两项叫做内项. 比例的性质:在比例中,两个外项的积等于两个内项的积,这叫做比例的基本性质. 如:4:5=16:20 4×20=5×16 2.正比例和反比例的意义 【知识点归纳】 1.正比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.如果用字母x和y表示这两种相关联的量,用k表示它们的比值(一定),正比例关系可以用式子表示为:k(一定). 2.反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系.如果用字母x和y表示这两种相关联的量, ... ...
~~ 您好,已阅读到文档的结尾了 ~~