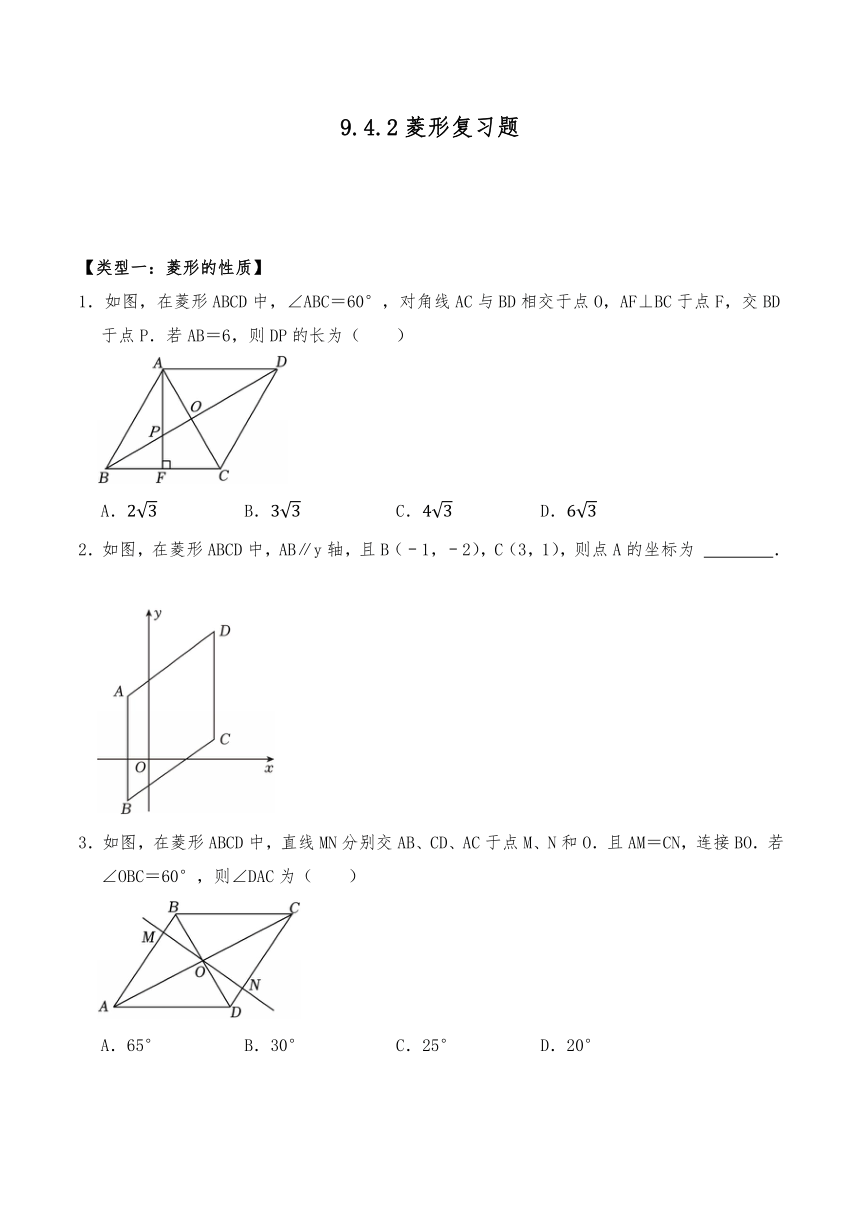
9.4.2菱形复习题 【类型一:菱形的性质】 1.如图,在菱形ABCD中,∠ABC=60°,对角线AC与BD相交于点O,AF⊥BC于点F,交BD于点P.若AB=6,则DP的长为( ) A. B. C. D. 2.如图,在菱形ABCD中,AB∥y轴,且B(﹣1,﹣2),C(3,1),则点A的坐标为 . 3.如图,在菱形ABCD中,直线MN分别交AB、CD、AC于点M、N和O.且AM=CN,连接BO.若∠OBC=60°,则∠DAC为( ) A.65° B.30° C.25° D.20° 4.如图,点O是菱形ABCD对角线的交点,CE∥BD,EB∥AC,连接OE. (1)求证:OE=CB; (2)如果OC:OB=2:1,,求菱形的面积. 【类型二:菱形的判定】 5.在四边形ABCD中,AD=BC,AB=CD.下列说法能使四边形ABCD为菱形的是( ) A.AC=BD B.∠C=∠D C.∠A=∠B D.AC⊥BD 6.如图,四边形ABCD中,AC和BD是对角线,依据图中所标的数据,下列四边形不一定为菱形的是( ) A. B. C. D. 7.一张矩形纸ABCD,将点B翻折到对角线AC上的点M处,折痕CE交AB于点E.将点D翻折到对角线AC上的点H处,折痕AF交DC于点F,折叠出四边形AECF. (1)求证:AF∥CE; (2)当∠BAC= 度时,四边形AECF是菱形?说明理由. 8.如图,四边形ABCD是平行四边形,O是对角线AC的中点,过点O的直线分别交边BC,AD于点E,F,连接AE,CF. (1)求证:BE=DF; (2)作∠AEB的平分线交AB于点G,若EG∥AC,求证:四边形AECF是菱形. 9.在 ABCD中,对角线AC与BD相交点O,过点O分别作AB和BC的垂线,垂足分别为H,M. (1)如图1,当OH=OM时,求证:平行四边形ABCD是菱形; (2)如图2,当∠ABC=90°时,若AB=OB,求的值. 【类型三:菱形的翻折问题】 10.如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为( ) A.78° B.75° C.60° D.45° 11.如图,菱形纸片ABCD的边长为2,点E在边AB上,将纸片沿CE折叠,点B落在B′处,CB'⊥AD,垂足为F.若∠B=60°,则BE的长是 . 【类型四:菱形的旋转问题】 12.如图,在平行四边形ABCD中,∠A=70°,将平行四边形ABCD绕顶点B顺时针旋转到平行四边形A1BC1D1,当C1D1首次经过顶点C时,旋转角∠ABA1=( ) A.30° B.40° C.45° D.60° 13.如图,菱形ABCD的边长为2,∠ABC=60°,对角线AC、BD交于点O.点E为直线AD上的一个动点,连接CE,将线段EC绕点C顺时针旋转∠BCD的角度后得到对应的线段CF(即∠ECF=∠BCD),DF长度的最小值为 . 【类型五:菱形的动点问题】 14.如图1,在菱形ABCD中,点P沿A﹣B﹣C方向从点A移动到点C,设点P的移动路程为x,线段AP的长为y,点P在运动过程中y与x的变化关系如图2所示,点P运动到BC边上时,当x=18,y的值最小为12,则a的值是 . 15.如图1,四边形ABCD是菱形,AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M,连接BM,且AH=3. (1)DH= ;DM= ; (2)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S,点P的运动时间为t秒,求S与t之间的函数关系式; (3)在(2)的条件下,当点P在边AB上运动时,是否存在这样的t的值,使∠MPB与∠BCD互为余角?若存在,求出t的值;若不存在,请说明理由. 【类型六:菱形在一次函数中的存在性问题】 16.已知,如图,O为坐标原点,在四边形OABC中,BC∥OA,BC=24,A(26,0),C(0,12),点D是OA的中点,动点P在线段BC上以每秒2个单位长度的速度由点C向B运动.设动点P的运动时间为t秒. (1)当P运动 秒,四边形PDAB是平行四边形. (2)在直线CB上是否存在一点Q,使得以O、D、Q、P四点为顶点的四边形是菱形?若存在, ... ...
~~ 您好,已阅读到文档的结尾了 ~~

