22.2二次函数abc符号问题 专项练习（含答案）人教版九年级数学上册

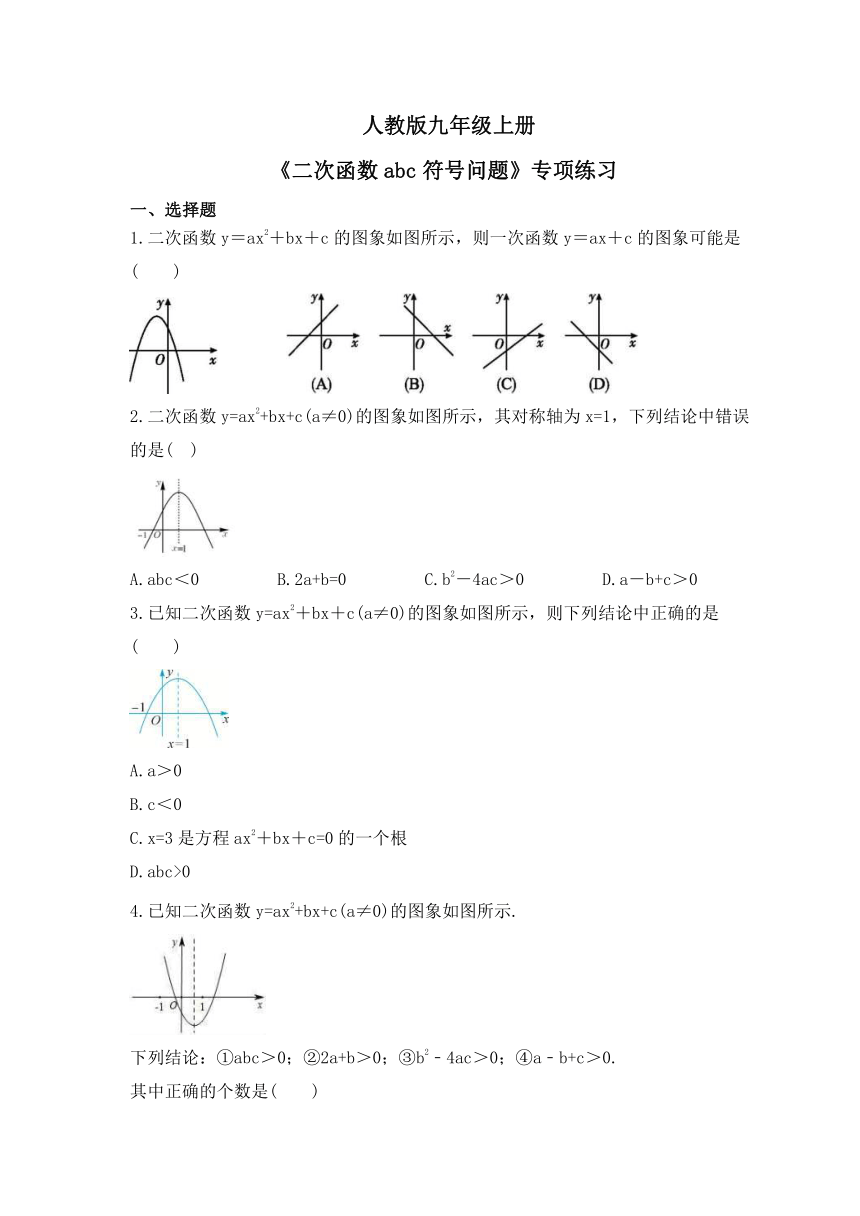
人教版九年级上册 《二次函数abc符号问题》专项练习 一 、选择题 1.二次函数y＝ax2＋bx＋c的图象如图所示，则一次函数y＝ax＋c的图象可能是(　　) 2.二次函数y=ax2+bx+c(a≠0)的图象如图所示，其对称轴为x=1，下列结论中错误的是( ) A.abc＜0 B.2a+b=0 C.b2－4ac＞0 D.a－b+c＞0 3.已知二次函数y=ax2＋bx＋c(a≠0)的图象如图所示，则下列结论中正确的是( ) A.a＞0 B.c＜0 C.x=3是方程ax2＋bx＋c=0的一个根 D.abc>0 4.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示. 下列结论：①abc＞0；②2a+b＞0；③b2﹣4ac＞0；④a﹣b+c＞0. 其中正确的个数是(　　) A.1 B.2 C.3 D.4 5.已知抛物线y=ax2+bx+c的图象如图所示,则|a﹣b+c|+|2a+b|=( ) A.a+b B.a﹣2b C.a﹣b D.3a 6.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示，并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根. 下列结论： ①b2﹣4ac＜0；②abc＞0；③a﹣b+c＜0；④m＞﹣2. 其中正确的个数有( ) A.1 B.2 C.3 D.4 7.关于x的方程x2﹣2mx＋4＝0有两个不同的实根，并且有一个根小于1，另一个根大于3，则实数m的取值范围为(　　) A.m＞ B.m＜﹣ C.m＜﹣2 或 m＞2 D.m＞ 8.已知抛物线y＝ax2＋bx＋c(a≠0)的对称轴为直线x＝2，与x轴的一个交点坐标为(4，0)，其部分图象如图所示，下列结论： ①抛物线过原点; ②4a＋b＋c＝0; ③a﹣b＋c＜0; ④抛物线的顶点坐标为(2，b); ⑤当x＜2时，y随x增大而增大. 其中结论正确的是(　　) A.①②③ B.③④⑤ C.①②④ D.①④⑤ 二 、填空题 9.若二次函数y=ax2+bx+c的图象如图所示，则直线y=abx+c不过第_____象限. 10.如图，抛物线y=ax2+bx+c(a>0)的对称轴是过点 (1，0)且平行于y轴的直线，若点P(4，0)在该抛物线上，则4a－2b+c的值为____. 11.已知二次函数y=ax2+bx+c的图象如图所示. 有以下结论： ①abc>0； ②a－b+c<0； ③2a=b； ④4a+2b+c>0； ⑤若点(－2,y1)和(,y2)在该图象上,则y1>y2. 其中正确的结论是　　　　(填入正确结论的序号). 12.如图，抛物线y＝ax2＋bx＋c(a，b，c是常数，a≠0)与x轴交于A，B两点，顶点P(m，n).给出下列结论： ①2a＋c＜0； ②若(﹣，y1)，(﹣，y2)，(，y3)在抛物线上，则y1＞y2＞y3； ③关于x的方程ax2＋bx＋k＝0有实数解，则k＞c﹣n. 其中正确结论是_____. 13.如图，二次函数y＝ax2＋bx＋c(a＞0)图象的顶点为D，其图象与x轴的交点A、B的横坐标分别为﹣1、3，与y轴负半轴交于点C. 在下面四个结论中： ①2a＋b＝0； ②c＝﹣3a； ③只有当a＝时，△ABD是等腰直角三角形； ④使△ACB为等腰三角形的a的值有三个. 其中正确的结论是　 　.(请把正确结论的序号都填上) 14.抛物线y＝ax2＋bx＋c的顶点为D(﹣1，2)，与x轴的一个交点A在点(﹣3，0)和(﹣2，0)之间，其部分图象如图，则以下结论：①b2﹣4ac＜0；②a＋b＋c＜0；③c﹣a＝2；④方程ax2＋bx＋c﹣2＝0有两个相等的实数根.其中正确的结论有　 　(填序号). 三 、解答题 15.已知抛物线y＝﹣x2＋bx＋c经过点(1,0)，（0，）. (1)求该抛物线的函数解析式； (2)将抛物线y＝﹣x2＋bx＋c平移，使其顶点恰好落在原点，请写出一种平移的方法及平移后的函数解析式. 16.已知二次函数y=(m﹣2)x2+(m+3)x+m+2的图象过点(0，5). (1)求m值，并写出二次函数的解析式. (2)求y的最小值. 17.如图，抛物线y＝x2＋bx＋c经过坐标原点，并与x轴交于点A(2，0). (1)求此抛物线的解析式; (2)求此抛物线顶点坐标及对称轴; (3)若抛物线上有一点B，且S△OAB＝1，求点B的坐标. 18.已知二次函数y＝ax2＋bx＋c(a<0)的部分图象如图所示,抛物线与x轴的一个交点坐标为(3,0),对称轴为直线x＝1. (1)若a＝﹣1,求c﹣b的值； (2)若实数m≠1,比较a＋b与m(am＋b)的大小,并说明理由. 19.如图，抛物线y=﹣x2+ ... ...