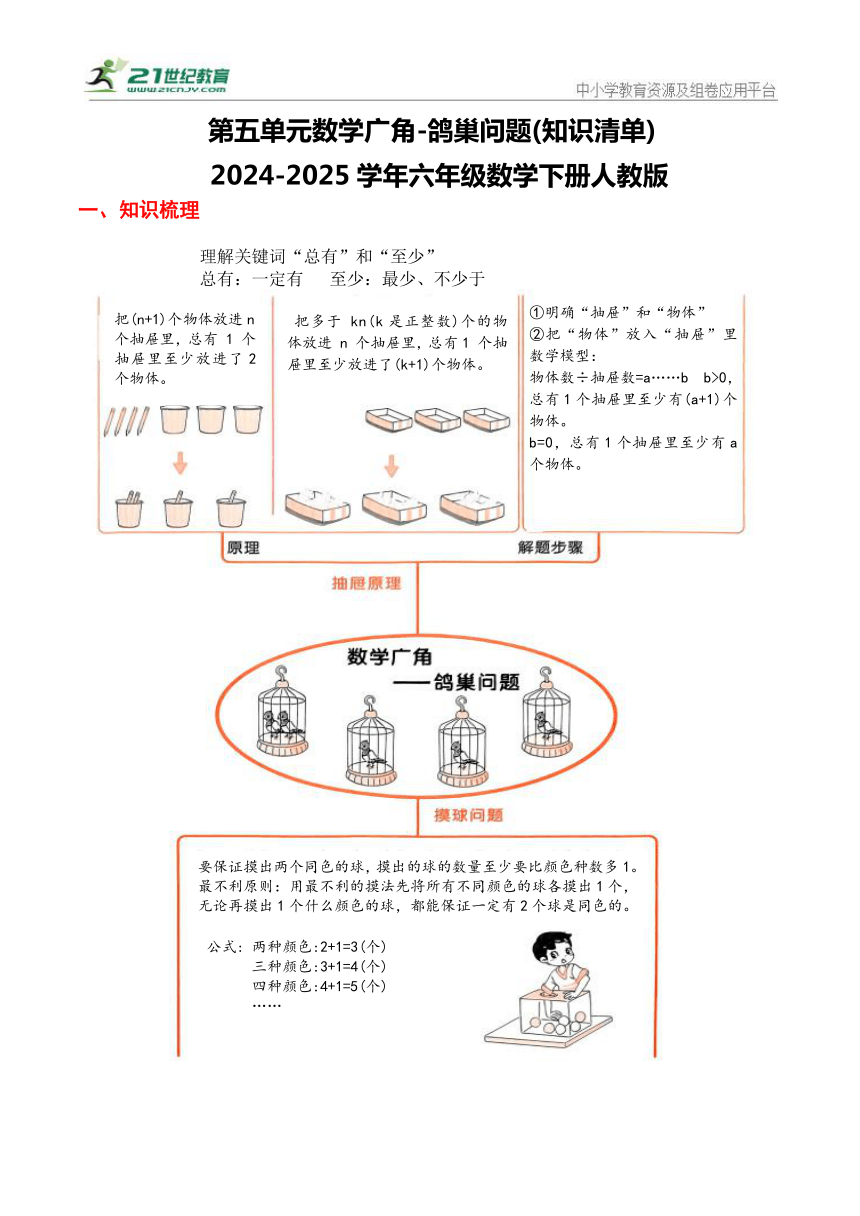
第五单元数学广角-鸽巢问题(知识清单)2024-2025学年六年级数学下册人教版

第五单元数学广角-鸽巢问题(知识清单) 2024-2025学年六年级数学下册人教版 知识梳理 理解关键词“总有”和“至少” 总有：一定有 至少：最少、不少于 常见题型 题型一：基本类型 解题方法：物体数÷鸽巢数=商……余数 至少数=商+1(有余数) 至少数=商(没余数) 1、7个苹果放进2个抽屉，总有一个抽屉里至少有几个苹果 7÷2=3 (个) ……1 (个) 3+1=4(个) 2、将23 支铅笔放进7个铅笔盒，最多的一个铅笔盒里至少有几支铅笔 23÷7=3 (支) ……2 (支) 3+1=4(支) 3、9个苹果放进3个盘中，总有一个盘中至少放几个苹果 9÷3=3(个) 题型二：构造鸽巢 解题方法：根据题意，构造鸽巢，得出鸽巢数量，再用鸽巢原理解答。 1、学校开设了画画、写作、书法3个兴趣班，四年级3 班共40人，每个学生都报名了其中两个兴趣班，那么这个班至少有多少个学生报的兴趣班完全一样 共有画画与写作，画画与书法，写作与书法3 种不同的组合, 也就是构造出3个鸽巢。40÷3=13 (个) ……1 (个) 13+1=14(个) 2、六年一班有 55 个学生，每个学生参加篮球、足球、排球中的一项或两项活动，那么至少多少人参加的活动项目相同 一项活动有3种，两项活动有3种组合，共6个鸽巢 55÷6=9 (个)……1 (个) 9+1=10 (个) 题型三： 求总数。(鸽子数) 解题方法：已知总有一个鸽巢里至少飞进n个鸽子，鸽子总量=鸽笼数量×(n-1)+1 1、圣诞节时圣诞老人给表现最好的 10 个小朋友送礼物，其中收到最多礼物的小朋友至少收到 3 件礼物，那么圣诞老人至少要准备多少件礼物 10× (3-1) +1=21 (件) 2、高老头让儿子小高去买馒头，分给高家庄上下老小40口人，请问小高至少要买多少个馒头，才能保证总有人至少能够分到5个馒头 40× (5-1) +1=161 (个) 3、把一些小蛋糕放进8个盒子里，要保证有一个盒子里至少有6块蛋糕，这些蛋糕至少有多少块 8× (6-1) +1=41(个) 题型四：求鸽巢数量 解题方法：已知总有一个鸽巢里至少飞进n个鸽子，鸽巢数量最多=(鸽子总量-1)÷(n-1) 1、将7支花插入一些花瓶里，要保证至少有一个花瓶里有2枝花，这些花瓶最多有多少个 (7-1) ÷ (2-1) =6 (个) 2、丁老师拿126个小礼物发给班里的所有学生，如果至少有一名学生拿到了 6 个小礼物，那么，李老师班里最多有多少名学生 (126-1) ÷ (6-1) =25 (名) 3、王叔叔要给房间的四壁涂上不同的颜色，可不管怎么涂，总有两面墙壁的颜色是一致的。李叔叔的颜料最多有几种颜色。 (4-1) ÷(2-1)=3(种) 题型五：生日问题。 解题方法：一年有12个月，相当于12个鸽巢，一年365天(平年)，相当于365个鸽巢。 1、15个小朋友中，至少有 ( )个小朋友在同一个月出生 15÷12=1 (个)…… 3 (个) 1+1=2(个) 有26名阿姨在跳广场舞，她们中至少有( )人的属相相同；共12种属相, 26÷12=2 (人) …… 2(人) 2+1=3 (人) 某校有 370 名 2020 年出生的学生，其中至少有几名学生的生日是同一天 2020年是瑞年,366天,370÷366=1(名)……4(名) 1+1=2(名) 题型六：摸球问题。 解题方法：用最不利原则思考问题，从最坏情况计算 1、求同色：所有颜色都拿一轮，再取一个可保证有相同颜色。 2、求不同色：最不利原则，把同一种颜色全部取完，再拿任何一个一定是不同颜色。 3、求某一种颜色：把其他颜色全部取完，再拿一个一定是目标颜色 1、【同色】把红、黄、蓝、白四种颜色的球各10个放到一个袋子里。至少取多少个球，可以保证取到两个颜色相同的球 最坏情况，4种颜色各取了1个，比4种颜色多1个，可保证有两个颜色相同 ， 4+1=5(个) 2【同色】盒子里有红球、蓝球和黄球各 6 个，至少要摸出( )个球一定有3个同色。 最坏情况，3种颜色的球平均取2个，再多取1个，可保证有3个同色, 3×2+1=7 (个) 3、【同色】在扑克牌的红桃、黑桃、方块、梅花各 13张不同点数， ... ...