小升初计算专题突破：平面图形计算-2024-2025学年数学六年级下册人教版（含解析）

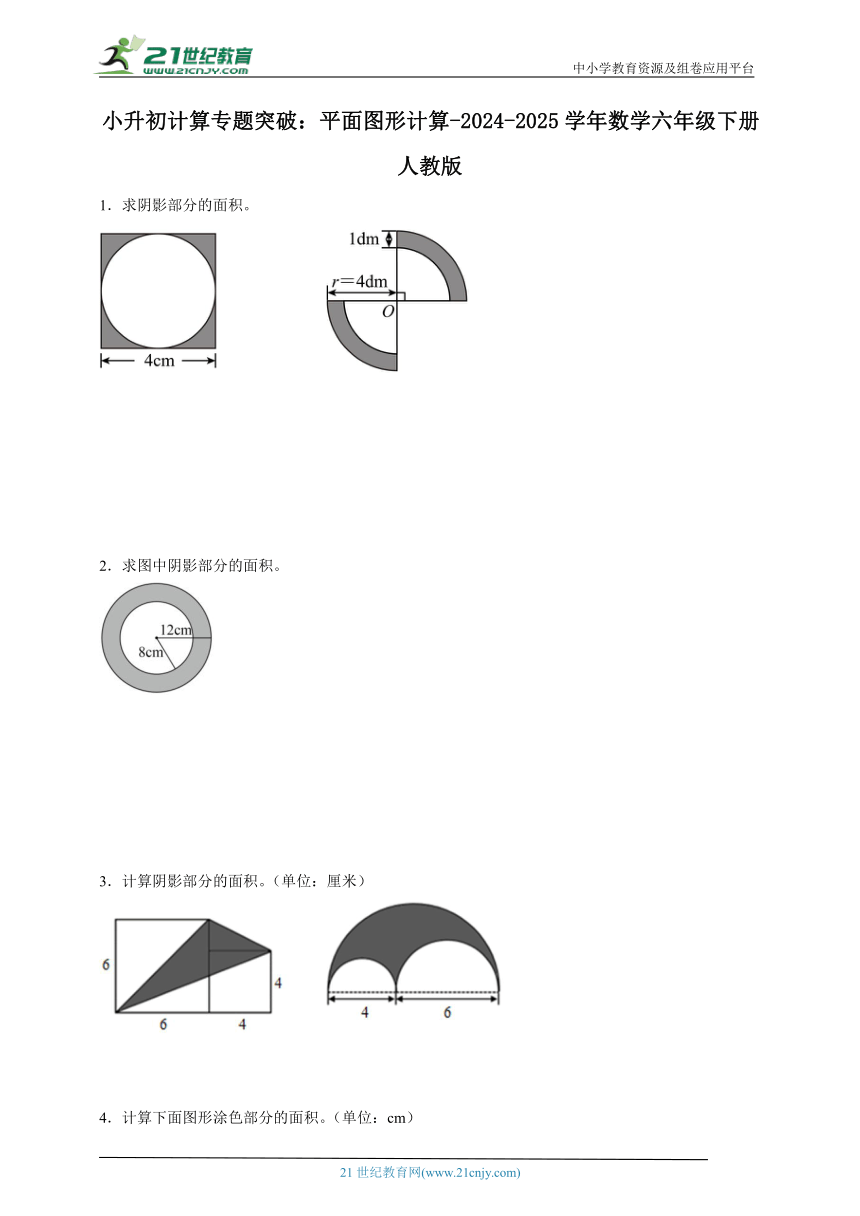
中小学教育资源及组卷应用平台 小升初计算专题突破：平面图形计算-2024-2025学年数学六年级下册人教版 1．求阴影部分的面积。 2．求图中阴影部分的面积。 3．计算阴影部分的面积。（单位：厘米） 4．计算下面图形涂色部分的面积。（单位：cm） 5．求下面组合图形的面积。（单位：dm） 6．计算下图阴影部分的面积。 7．如图，已知正方形边长是4dm，求阴影部分的面积。 8．计算阴影部分的面积。 9．求如图图形中阴影部分的周长和面积。（单位：厘米） 10．计算如图阴影部分的面积。（单位：cm） 11．求下图中阴影部分的面积。 12．求涂色部分的面积。（单位：cm） 13．求下面各图形中涂色部分的面积。 14．求下面阴影部分的面积。（单位：厘米） 15．计算图中阴影部分的面积。 16．求下图阴影部分的面积。（单位：厘米） 17．求涂色部分的周长和面积。（单位：分米） 18．求阴影部分的面积。 19．图形与计算。 求阴影部分的面积。 20．求下图阴影部分的周长。 21．计算下面图形中涂色部分的周长和面积。 《小升初计算专题突破：平面图形计算-2024-2025学年数学六年级下册人教版》参考答案 1．3.44cm2；10.99dm2 【分析】（1）观察图形可知，阴影部分的面积＝正方形的面积－圆的面积，根据正方形的面积公式S＝a2，圆的面积公式S＝πr2，代入数据计算求出阴影部分的面积。 （2）观察图形，阴影部分可以组成一个半圆环，根据半圆环的面积公式S环＝π（R2－r2）÷2，代入数据计算求出阴影部分的面积。 【详解】（1）4×4－3.14×（4÷2）2 ＝4×4－3.14×22 ＝4×4－3.14×4 ＝16－12.56 ＝3.44（cm2） 阴影部分的面积是3.44cm2。 （2）4－1＝3（dm） 3.14×（42－32）÷2 ＝3.14×（16－9）÷2 ＝3.14×7÷2 ＝10.99（dm2） 阴影部分的面积是10.99dm2。 2．251.2cm2 【分析】观察图形可知，阴影部分是一个圆环，根据圆环的面积公式S环＝π（R2－r2），代入数据计算求出阴影部分的面积。 【详解】3.14×（122－82） ＝3.14×（144－64） ＝3.14×80 ＝251.2（cm2） 阴影部分的面积是251.2cm2。 3．18平方厘米；18.84平方厘米 【分析】（1）观察图形，把图形补成一个长（6＋4）厘米、宽为6厘米的大长方形，那么阴影部分的面积＝大长方形的面积－①的面积－②的面积－③的面积，根据长方形的面积＝长×宽，三角形的面积＝底×高÷2，代入数据计算求出阴影部分的面积。 （2）观察图形可知，阴影部分的面积＝直径为（4＋6）厘米的半圆的面积－直径为4厘米的半圆的面积－直径为6厘米的半圆的面积，根据圆的面积公式S＝πr2，代入数据计算求出阴影部分的面积。 【详解】（1）（6＋4）×6－6×6÷2－（6＋4）×4÷2－4×（6－4）÷2 ＝10×6－6×6÷2－10×4÷2－4×2÷2 ＝60－18－20－4 ＝18（平方厘米） 阴影部分的面积是18平方厘米。 （2）（4＋6）÷2 ＝10÷2 ＝5（厘米） 4÷2＝2（厘米） 6÷2＝3（厘米） 3.14×52÷2－3.14×22÷2－3.14×32÷2 ＝3.14×25÷2－3.14×4÷2－3.14×9÷2 ＝39.25－6.28－14.13 ＝18.84（平方厘米） 阴影部分的面积是18.84平方厘米。 4．48cm2；20cm2 【分析】（1）阴影部分的面积＝长方形的面积－空白部分三角形的面积，三角形的底和高分别就是长方形的宽和长，即三角形的面积就是长方形面积的一半，则阴影部分的面积也是长方形面积的一半。 （2）将图形分成一个底是4，高是4的直角三角形和一个长是6，宽是2的长方形，再根据三角形的面积＝底×高÷2和长方形的面积＝长×宽，代入数据计算即可。 【详解】8×12÷2 ＝8×6 ＝48（cm2） 则阴影部分的面积是48cm2。 2＋2＝4（cm） 10－6＝4（cm） 4×4÷2＝8（cm2） 2×6＝12（cm2） 8＋12＝20（cm2） 则阴影部分的面积是20cm2。 5．31dm2 【分析】观察图 ... ...