2025年九年级数学中考三轮冲刺训练高频考点四边形中的三角函数综合题练习（含解析）

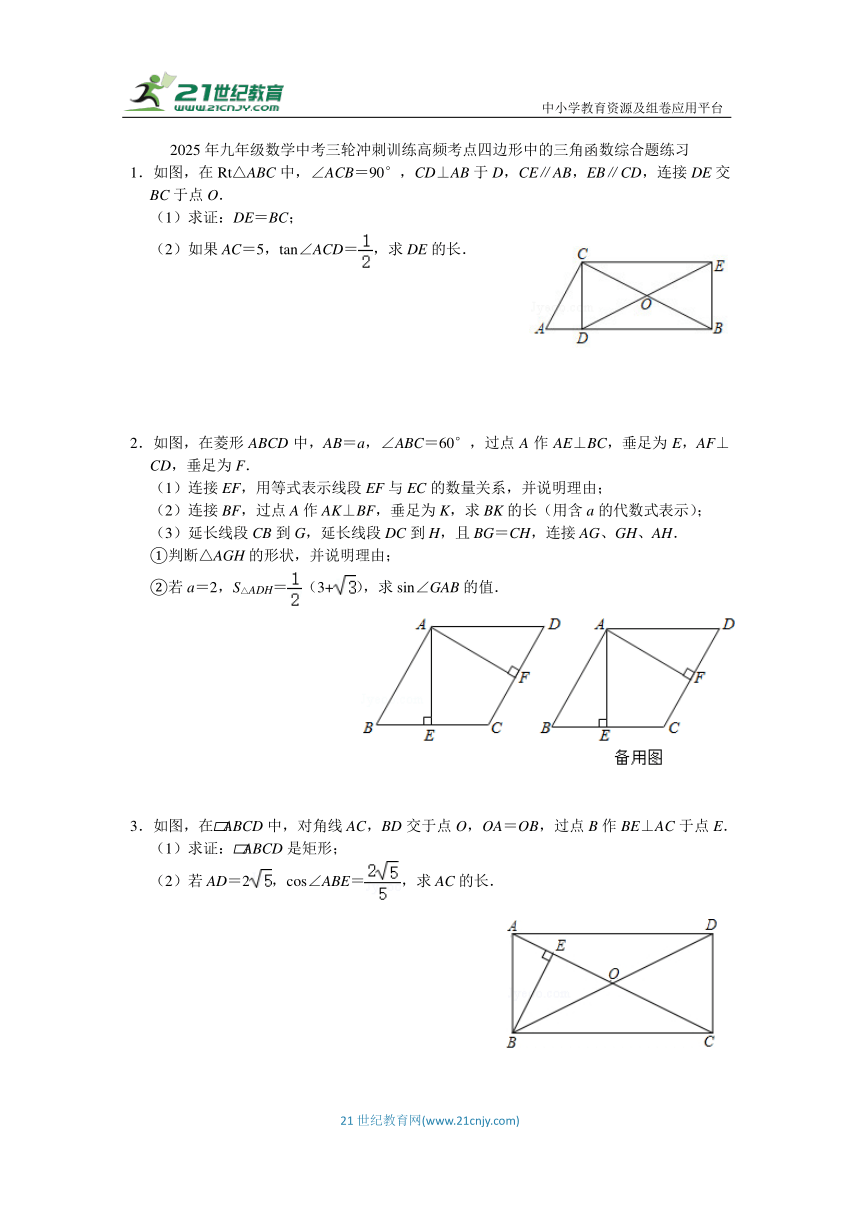
中小学教育资源及组卷应用平台 2025年九年级数学中考三轮冲刺训练高频考点四边形中的三角函数综合题练习 1．如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于D，CE∥AB，EB∥CD，连接DE交BC于点O． （1）求证：DE＝BC； （2）如果AC＝5，tan∠ACD＝，求DE的长． 2．如图，在菱形ABCD中，AB＝a，∠ABC＝60°，过点A作AE⊥BC，垂足为E，AF⊥CD，垂足为F． （1）连接EF，用等式表示线段EF与EC的数量关系，并说明理由； （2）连接BF，过点A作AK⊥BF，垂足为K，求BK的长（用含a的代数式表示）； （3）延长线段CB到G，延长线段DC到H，且BG＝CH，连接AG、GH、AH． ①判断△AGH的形状，并说明理由； ②若a＝2，S△ADH＝（3+），求sin∠GAB的值． 3．如图，在 ABCD中，对角线AC，BD交于点O，OA＝OB，过点B作BE⊥AC于点E． （1）求证： ABCD是矩形； （2）若AD＝2，cos∠ABE＝，求AC的长． 4．如图，矩形ABCD的对角线AC，BD相交于点O，过B点作BF∥AC，过C点作CF∥BD，BF与CF相交于点F． （1）求证：四边形BFCO是菱形； （2）连接OF、DF，若AB＝2，tan∠OFD＝，求AC的长． 5．如图，在 ABCD中，AC，BD交于点O，且AO＝BO． （1）求证：四边形ABCD是矩形； （2）∠ADB的角平分线DE交AB于点E，当AD＝3，tan∠CAB＝时，求AE的长． 6．如图1，在矩形ABCD中，AB＝6，BC＝8，点E是对角线BD的中点，直角∠GEF的两直角边EF、EG分别交CD、BC于点F、G． （1）若点F是边CD的中点，求EG的长． （2）当直角∠GEF绕直角顶点E旋转，旋转过程中与边CD、BC交于点F、G．∠EFG的大小是否发生变化？如果变化，请说明理由；如果不变，请求出tan∠EFG的值． （3）当直角∠GEF绕顶点E旋转，旋转过程中与边CD、BC所在的直线交于点F、G．在图2中画出图形，并判断∠EFG的大小是否发生变化？如果变化，请说明理由；如果不变，请直接写出tan∠EFG的值． （4）如图3，连接CE交FG于点H，若＝，请求出CF的长． 7．如图，在平行四边形ABCD中，AB＝5，BC＝10，F为AD的中点，CE⊥AB于E，设∠ABC＝α（60°≤α＜90°）． （1）当α＝60°时，求CE的长； （2）当60°＜α＜90°时， ①求证：∠EFD＝3∠AEF； ②当CE2﹣EF2取最大值时，求sin∠B的值． 8．已知，四边形ABCD是正方形，点E是AD边上任意一点，点F是AB边上任意一点，DF⊥CE于点G． （1）如图1，求证：BF＝AE； （2）如图2，连接BG，若tan∠ADF＝，EG＝1，求BG的长． 9．如图，在直角△ABC中，∠ACB＝90°，CD⊥AB，垂足为D，O是BC边中点，连结DO并延长到点E，使OE＝OD，连结BE，CE． （1）求证：四边形CDBE为矩形． （2）若tanA＝2，AD＝5，求线段BE的长． 10．如图， ABCD的两条对角线相交于O点，过O点作OE⊥AB，垂足为E，已知∠DBA＝∠DBC，AB＝5． （1）求证：四边形ABCD为菱形； （2）若sin∠ADB＝，求线段OE的长． 11．如图，矩形ABCD对角线相交于O点，DE∥AC，CE∥BD，连接BE． （1）求证：四边形OCED是菱形； （2）若∠AOD＝120°，CD＝2，求DE和tan∠DBE的值． 12．在平行四边形ABCD中，过点A作AE⊥BC于点E，点F在边AD上，且DF＝BE，连接DE，CF． （1）求证：四边形AECF是矩形； （2）若DE平分∠ADC，AB＝5，AD＝8，求tan∠ADE的值． 13．【性质探究】 如图，在矩形ABCD中，对角线AC，BD相交于点O，AE平分∠BAC，交BC于点E．作DF⊥AE于点H，分别交AB，AC于点F，G． （1）判断△AFG的形状并说明理由． （2）求证：BF＝2OG． 【迁移应用】 （3）记△DGO的面积为S1，△DBF的面积为S2，当＝时，求的值． 【拓展延伸】 （4）若DF交射线AB于点F，【性质探究】中的其余条件不变，连结EF，当△BEF的面积为矩形ABCD面积的时，请直接写出tan∠BAE的值． 14．如图，在正方形ABCD中，分别过顶点B，D作BE∥DF交对角线AC所在直线 ... ...