9.1图形的旋转同步强化练习（含解析）

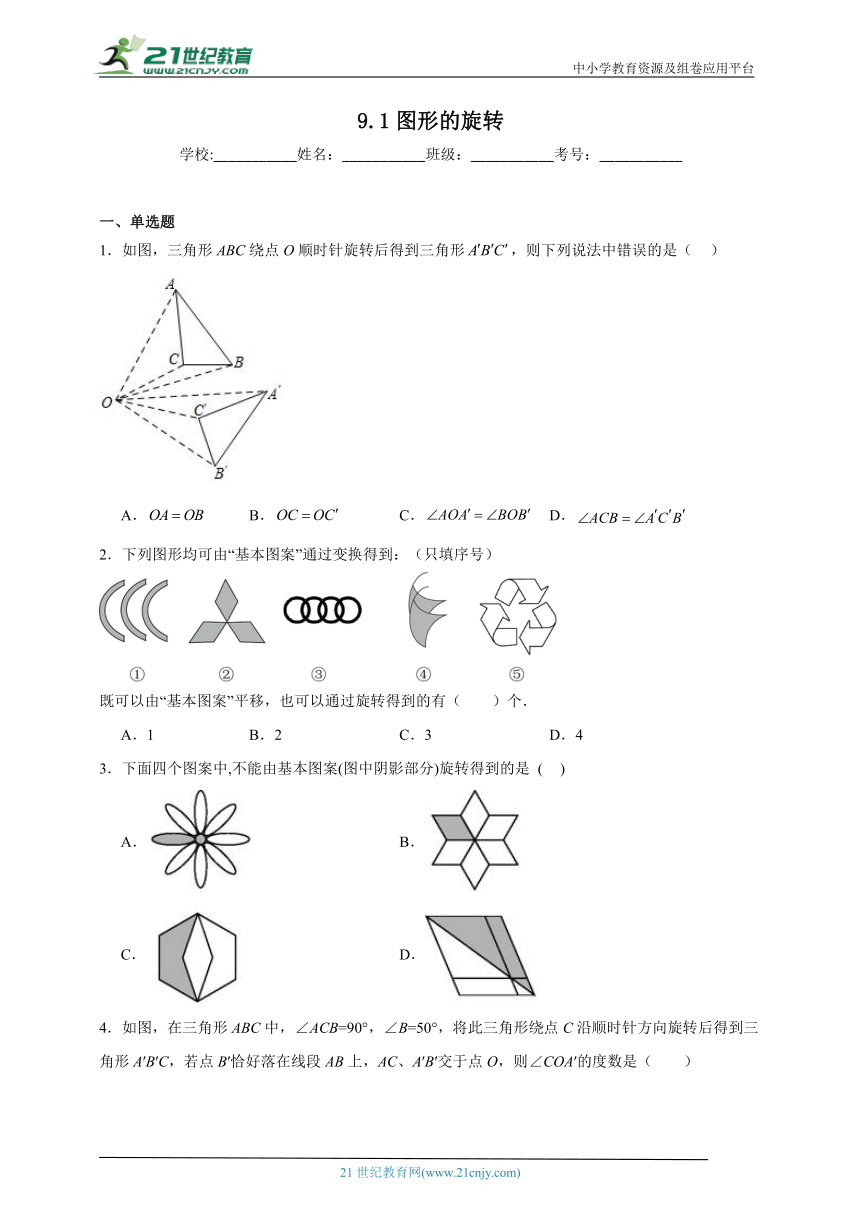
中小学教育资源及组卷应用平台 9.1图形的旋转 学校:_____姓名：_____班级：_____考号：_____ 一、单选题 1．如图，三角形ABC绕点O顺时针旋转后得到三角形，则下列说法中错误的是（ ） A． B． C． D． 2．下列图形均可由“基本图案”通过变换得到：（只填序号） 既可以由“基本图案”平移，也可以通过旋转得到的有（　　）个． A．1 B．2 C．3 D．4 3．下面四个图案中,不能由基本图案(图中阴影部分)旋转得到的是 ( ) A． B． C． D． 4．如图，在三角形ABC中，∠ACB=90°，∠B=50°，将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C，若点B′恰好落在线段AB上，AC、A′B′交于点O，则∠COA′的度数是（　　） A．50° B．60° C．70° D．80° 5．下列四个图形中，形成方法与另外三个不同的是（ ）． A． B． C． D． 6．如图，直线：交轴于，交轴于，轴上一点，为轴上一动点，把线段绕点逆时针旋转得到线段，连接，，则当长度最小时，线段的长为（ ） A． B． C．5 D． 7．在下图右侧的四个三角形中，不能由左侧的三角形经过旋转或平移得到的是(　　) A．A B．B C．C D．D 8．如图，在等边△ABC中，AC＝9，点O在AC上，且AO＝3，点P是AB上一动点，连结OP，将线段OP绕点O逆时针旋转60°得到线段OD．要使点D恰好落在BC上，则AP的长是（ ） A．2 B．3 C．5 D．6 9．在中，，点D为中点，，绕点D旋转，分别与边交于E，F两点．下列结论：①；②；③；④始终为等腰直角三角形，其中正确的个数有（ ）． A．1个 B．2个 C．3个 D．4个 10．如图，在的正方形网格中，由旋转得到，其旋转中心是（ ） A．点 B．点 C．点 D．点 11．一个图形经过旋转变换，下列说法中：①对应线段平行；②对应线段相等；③对应角相等；④图形的形状和大小都没有改变．正确的个数有（　　） A．1个 B．2个 C．3个 D．4个 12．如图，将三角形ABC绕着点C顺时针旋转60°后得到三角形A′B′C，若∠A=40°，∠B=110°，则∠A′CB′的度数是（ ） A． B． C． D． 二、填空题 13．如图，在Rt△ABC中，已知：∠C=90°，∠A=60°，AC=3cm，以斜边AB的中点P为旋转中心，把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′，则旋转前后两个直角三角形重叠部分的面积为 ． 14．等边绕其外心旋转，至少要旋转 度才能与原图形重合． 15．有如图，从图形甲到图形乙，所进行的图形运动是先绕点 时针旋转，再向右移动 格． 16．在正方形、长方形、线段、等边三角形和平行四边形这五种图形中，是旋转对称图形不是中心对称图形的是 . 17．正九边形绕它的旋转中心至少旋转　　　　°后才能与原图形重合. 三、解答题 18．如图，点A在射线OX上，OA的长等于2cm.如果OA绕点O，按逆时针方向旋转30°到 ，那么点的位置可以用（2，30°）表示.如果将再沿逆时针方向继续旋转45°，到，那么点的位置可以用（ ， ）表示. 19．如图1所示，将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起，构成一个大的长方形ABEF．现将小长方形CEFD绕点C顺时针旋转至，旋转角为． （1）当点′恰好落在EF边上时，求旋转角的值； （2）如图2，G为BC的中点，且0°＜＜90°，求证：； （3）小长方形CEFD绕点C顺时针旋转一周的过程中，与能否全等？若能，直接写出旋转角的值；若不能，说明理由． 20．如图，点、的坐标分别为、．将绕点按逆时针方向旋转得到． (1)画出： (2)写出点、的坐标． 21．已知△ABC是边长为4的等边三角形，边AB在射线OM上，且OA＝6，点D是射线OM上的动点，当点D不与点A重合时，将△ACD绕点C逆时针方向旋转60°得到△BCE，连接DE，设OD＝m． （1）问题发现 如图1，△CDE的形状是_____三角形． （2）探究证明 如图2，当6＜m＜10时，△BDE的周长是否存在最小值？若 ... ...