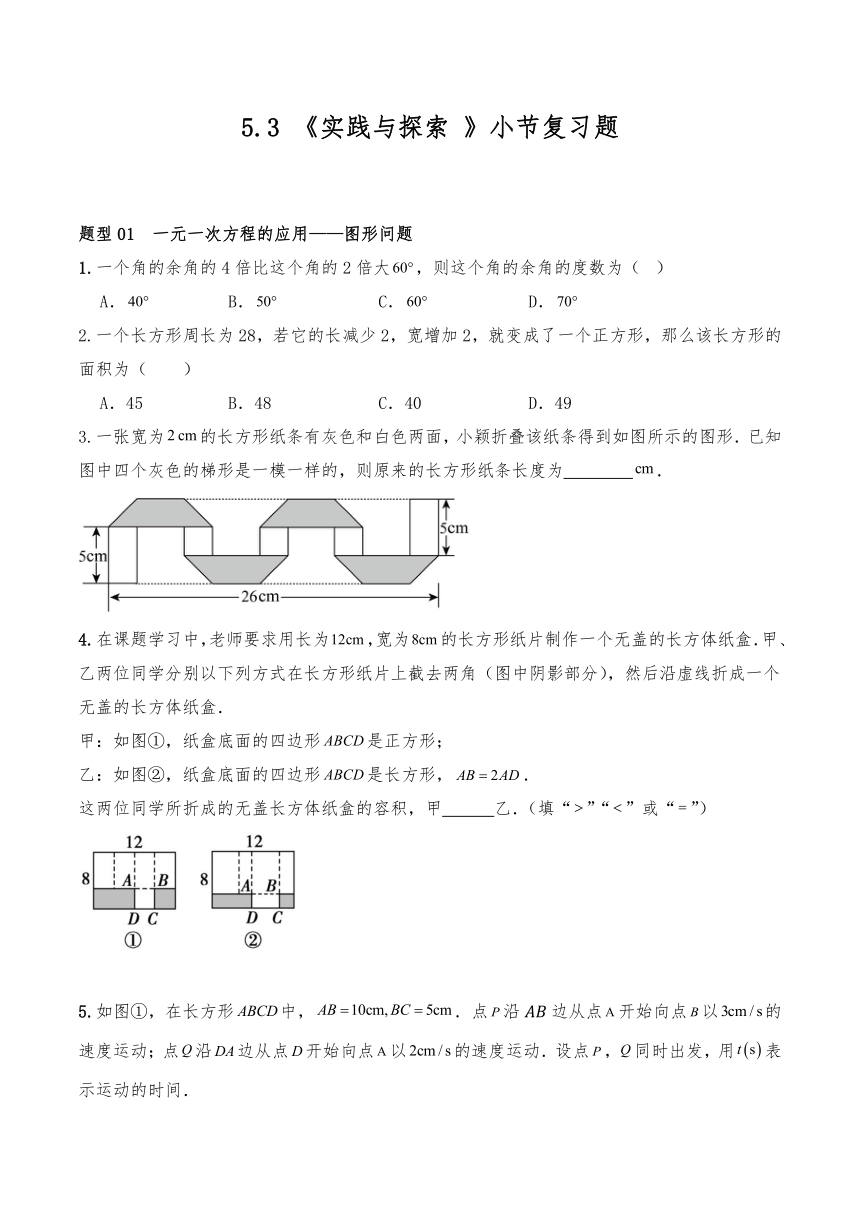
5.3 《实践与探索 》小节复习题 题型01 一元一次方程的应用———图形问题 1.一个角的余角的4倍比这个角的2倍大,则这个角的余角的度数为( ) A. B. C. D. 2.一个长方形周长为28,若它的长减少2,宽增加2,就变成了一个正方形,那么该长方形的面积为( ) A.45 B.48 C.40 D.49 3.一张宽为的长方形纸条有灰色和白色两面,小颖折叠该纸条得到如图所示的图形.已知图中四个灰色的梯形是一模一样的,则原来的长方形纸条长度为 . 4.在课题学习中,老师要求用长为,宽为的长方形纸片制作一个无盖的长方体纸盒.甲、乙两位同学分别以下列方式在长方形纸片上截去两角(图中阴影部分),然后沿虚线折成一个无盖的长方体纸盒. 甲:如图①,纸盒底面的四边形是正方形; 乙:如图②,纸盒底面的四边形是长方形,. 这两位同学所折成的无盖长方体纸盒的容积,甲 乙.(填“”“”或“”) 5.如图①,在长方形中,.点沿边从点开始向点以的速度运动;点沿边从点开始向点以的速度运动.设点,同时出发,用表示运动的时间. 【发现】_____,_____. (用含的代数式表示) 【拓展】如图①,当_____时,线段与线段相等; 【探究】若点,分别到达点,后继续沿着的方向运动,当点与点第一次相遇时,请写出相遇点的位置,并说明理由. 题型02 一元一次方程的应用———销售问题 1.某商场以50元每件的价格购进一批衬衫,以标价75元的价格进行销售.赶上换季,商场进行打折销售,每件仍可获利10元,则商场是以_____折进行销售( ) A.八五 B.七五 C.八 D.七 2.某种商品每件的售价比进价多,在“双十一”期间每件又降价10元卖出,结果每件获利5元,这种商品每件的进价是多少元?设每件商品的进价是元,那么所列方程为( ) A. B. C. D. 3.某电商平台决定举办“跨年”促销活动,对网上销售的某种蓝牙耳机按成本价提高后标价,又以九折优惠卖出,结果每个耳机仍可获利8元,若设这种耳机每件的成本为a元,则可列方程: . 4.某工厂甲乙两个车间计划每月生产3600个零件,上月甲车间产量比原计划增长了,乙车间产量比原计划增长了,因此两车间共生产了4000个零件,那么甲、乙车间上月实际生产的零件数分别是 . 5.双十二将近,互联网电商纷纷推出多种促销方式吸引顾客让利消费者.某电商商品标价每件元,推出了如下的优惠促销活动: 打折前一次性购物总金额 优惠措施 少于或等于元 一律打八折 超过元,但不超过元 一律打七折 超过元 其中元部分打五折,超过元的部分打三折优惠 (1)张老师一次性购买该商品件,实际付款多少元? (2)李老师一次性购买该商品若干件,实际付款元,请认真思考求出李老师购买该商品所有可能的件数. 题型03 一元一次方程的应用———工程问题 1.一个道路工程,甲队单独施工9天完成,乙队单独施工24天完成.现在甲乙两队共同施工3天,因甲另有任务,剩下的工程由乙队完成,乙队还需( )天才能完成. A.13 B.14 C.15 D.16 2.装订一批书,计划每天装订1800本,40天完成,实际每天装订2000本,实际几天可以完成?解答时设实际x天可以完成,正确的列式是( ) A. B. C. D. 3.制造一批零件,按计划18天可以完成它的.如果工作4天后,工作效率提高了,那么完成这批零件的一半,一共需要 天. 4.某厂接受为四川灾区生产活动板房的任务,计划在30天内完成,若每天多生产6套,则25天完成且还多生产10套,问原计划每天生产多少套板房?设原计划每天生产x套,列方程式是 . 5.哈市有甲乙两个工程队,现有一小区需要进行小区改造,甲工程队单独完成这一项工程需要20天,乙工程队单独完成这项工程所需的时间比甲工程队多. (1)求乙队单独完成这项工程需要多少天? (2)现在若甲工程队先做5天,剩余部分再由甲乙 ... ...
~~ 您好,已阅读到文档的结尾了 ~~